5.6. Extremos (relativos y absolutos) con Python#

Esta sección pretende ser un compendio (esperemos que claro y ordenado) de todo el Python que hemos ido usando en las tres últimas secciones del Capítulo 3.

5.6.1. Cálculo de extremos relativos con Python#

Mostramos, sobre un ejemplo, cómo se localizan los puntos críticos y como se clasifican, con la ayuda de Python.

En este caso, buscamos los puntos críticos de la función \(f(x,y) = -x^3 + 4xy - 2y^2 +1\) en todo \(\mathbb{R}^2\).

Como ya dijimos en la sección correspondiente del capítulo 3, aquí está hecho un poco de andar por casa. Te planteamos como reto escribir una function que clasifique automáticamente los puntos críticos… ¿Lo has hecho?

import sympy as sp
import numpy as np

x, y = sp.symbols('x y', real=True) # define as variables simbólicas x e y
f = sp.Lambda((x,y), -x**3 +4*x*y-2*y**2+1)

# Calculamos el gradiente de f
grad_f =  sp.transpose(sp.Matrix([f(x,y)]).jacobian([x,y]))
display(grad_f)

# Buscamos los puntos críticos
sol = sp.solve((sp.Eq(grad_f[0],0),sp.Eq(grad_f[1],0)),(x,y), dict=True)
display('Puntos críticos:', sol)

# Definimos la hessiana son sp.hessian
H = sp.Lambda((x,y), sp.hessian(f(x,y), (x,y)))
display('Matriz hessiana en (x,y): ', H(x,y))

# Clasificación del primer punto crítico
H0 = H(sol[0][x],sol[0][y])
display('Hessiana del primer punto crítico: ', H0)
print("Determinante: ",sp.det(H0), ". Posición (1,1):", H0[0,0])

# Clasificación del segundo punto crítico
H1 = H(sol[1][x],sol[1][y])
display('Hessiana del segundo punto crítico: ', H1)
print("Determinante: ",sp.det(H1), ". Posición (1,1):", H1[0,0])
\[\begin{split}\displaystyle \left[\begin{matrix}- 3 x^{2} + 4 y\\4 x - 4 y\end{matrix}\right]\end{split}\]
'Puntos críticos:'

[{x: 0, y: 0}, {x: 4/3, y: 4/3}]

'Matriz hessiana en (x,y): '
\[\begin{split}\displaystyle \left[\begin{matrix}- 6 x & 4\\4 & -4\end{matrix}\right]\end{split}\]
'Hessiana del primer punto crítico: '
\[\begin{split}\displaystyle \left[\begin{matrix}0 & 4\\4 & -4\end{matrix}\right]\end{split}\]
Determinante:  -16 . Posición (1,1): 0

'Hessiana del segundo punto crítico: '
\[\begin{split}\displaystyle \left[\begin{matrix}-8 & 4\\4 & -4\end{matrix}\right]\end{split}\]
Determinante:  16 . Posición (1,1): -8

5.6.2. Cálculo de extremos absolutos sobre una restricción#

Aquí mostramoscómo implementar, con la ayuda de Python, el método de los multiplicadores de Lagrange. Lo hacemos sobre un ejemplo:

Example (Máximo absoluto en la piel de la elipse)

Calcular el máximo absoluto de

\[ f(x,y) = 4xy \]

en el conjunto

\[ C = \left\{ (x,y) \in\mathbb{R}^{2} : \frac{x^2}{3^2} + \frac{y^2}{4^2} = 1 \right\}. \]
import sympy as sp

x, y, l = sp.symbols('x y l', real=True) # definimos las variables simbólicas x, y, l
f = sp.Lambda((x,y), 4*x*y) # función a optimizar
g = sp.Lambda((x,y), x**2/9 + y**2/16) # restricción

# Cálculo de puntos críticos (posibles extremos globales)
grad_f =  sp.transpose(sp.Matrix([f(x,y)]).jacobian([x,y]))
grad_g = sp.transpose(sp.Matrix([g(x,y)]).jacobian([x,y]))
sol = sp.solve((sp.Eq(grad_f[0],l*grad_g[0]),sp.Eq(grad_f[1],l*grad_g[1]),sp.Eq(g(x,y),1)), 
               (x,y,l), dict=True)

for p in sol:
    print('Punto crítico (x,y,lambda)=',p,'; f(x,y)=', sp.N(f(p[x],p[y])))

Punto crítico (x,y,lambda)= {l: -24, x: -3*sqrt(2)/2, y: 2*sqrt(2)} ; f(x,y)= -24.0000000000000
Punto crítico (x,y,lambda)= {l: -24, x: 3*sqrt(2)/2, y: -2*sqrt(2)} ; f(x,y)= -24.0000000000000
Punto crítico (x,y,lambda)= {l: 24, x: -3*sqrt(2)/2, y: -2*sqrt(2)} ; f(x,y)= 24.0000000000000
Punto crítico (x,y,lambda)= {l: 24, x: 3*sqrt(2)/2, y: 2*sqrt(2)} ; f(x,y)= 24.0000000000000

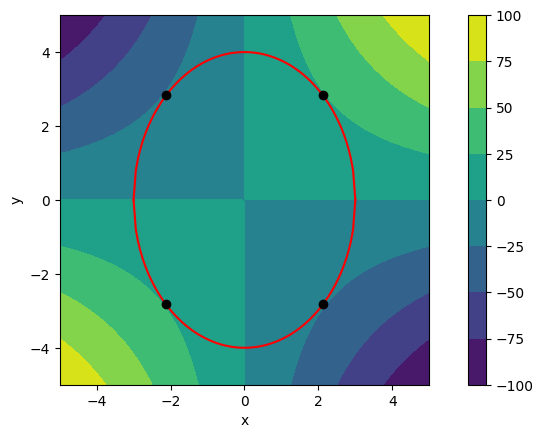
Visualizamos estos puntos críticos sobre las curvas de nivel:

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# Nube de puntos para el cálculo de las curvas de nivel
N = 100  
xvec = np.linspace(-5, 5, N)
yvec = np.linspace(-5, 5, N)
X, Y = np.meshgrid(xvec, yvec)
F = sp.lambdify((x,y),f(x,y),"numpy")

# Representación gráfica de f
plt.contourf(X, Y, F(X,Y))
plt.colorbar()  
plt.xlabel('x')
plt.ylabel('y')
plt.axis('square')

# Representación gráfica de la restricción
xvec = np.linspace(-3, 3, N)
sol_curve = sp.solve(sp.Eq(g(x,y),1),y) # despejar y en función de x en g(x,y)=1
for c in sol_curve:
    curve = sp.lambdify(x,c,"numpy")
    plt.plot(xvec, curve(xvec),'r')

# Representación gráfica de los extremos relativos
for p in sol:
    plt.plot(p[x],p[y],'ko')

plt.show()
../../_images/06.Extremos_6_0.png

5.6.3. Cálculo de extremos absolutos sobre interior y frontera#

En este caso queremos

Example (Máximo absoluto en la elipse: interior + piel)

Calcular el máximo absoluto de

\[ f(x,y) = 4xy \]

en el conjunto

\[ C = \left\{ (x,y) \in\mathbb{R}^{2} : \frac{x^2}{3^2} + \frac{y^2}{4^2} \leq 1 \right\}. \]
import sympy as sp

x, y, l = sp.symbols('x y l', real=True) # definimos las variables simbólicas x, y, l
f = sp.Lambda((x,y), 4*x*y) # función a optimizar
g = sp.Lambda((x,y), x**2/9 + y**2/16) # restricción

# Primer paso: puntos críticos de f en el interior de la elipse
grad_f =  sp.transpose(sp.Matrix([f(x,y)]).jacobian([x,y]))
sol1 = sp.solve((sp.Eq(grad_f[0],0),sp.Eq(grad_f[1],0)),(x,y), dict=True)

# Segundo paso: posibles extremos en la frontera de la elipse
grad_g = sp.transpose(sp.Matrix([g(x,y)]).jacobian([x,y]))
sol2= sp.solve((sp.Eq(grad_f[0],l*grad_g[0]),sp.Eq(grad_f[1],l*grad_g[1]),sp.Eq(g(x,y),1)), 
               (x,y,l), dict=True)

sol = sol1 + sol2

for p in sol:
    print('Punto crítico (x,y,lambda)=',p,'; f(x,y)=', sp.N(f(p[x],p[y])))

Punto crítico (x,y,lambda)= {y: 0, x: 0} ; f(x,y)= 0
Punto crítico (x,y,lambda)= {l: -24, x: -3*sqrt(2)/2, y: 2*sqrt(2)} ; f(x,y)= -24.0000000000000
Punto crítico (x,y,lambda)= {l: -24, x: 3*sqrt(2)/2, y: -2*sqrt(2)} ; f(x,y)= -24.0000000000000
Punto crítico (x,y,lambda)= {l: 24, x: -3*sqrt(2)/2, y: -2*sqrt(2)} ; f(x,y)= 24.0000000000000
Punto crítico (x,y,lambda)= {l: 24, x: 3*sqrt(2)/2, y: 2*sqrt(2)} ; f(x,y)= 24.0000000000000