3.3. Diferenciabilidad

3.3.1. Definición de diferenciabilidad

Comenzaremos esta sección motivando la aparición de un concepto más fuerte que el asociado a la existencia de las derivadas parciales, que resulta ser el concepto de diferenciabilidad.

En primer lugar, debemos entender que, para funciones de dos o más variables, la existencia de las derivadas parciales (es decir, la derivabilidad en la dirección de los ejes) no garantiza la existencia de otras derivadas direccionales. Es más, ni siquiera garantiza la continuidad.

Vamos a verlo sobre un ejemplo:

Example

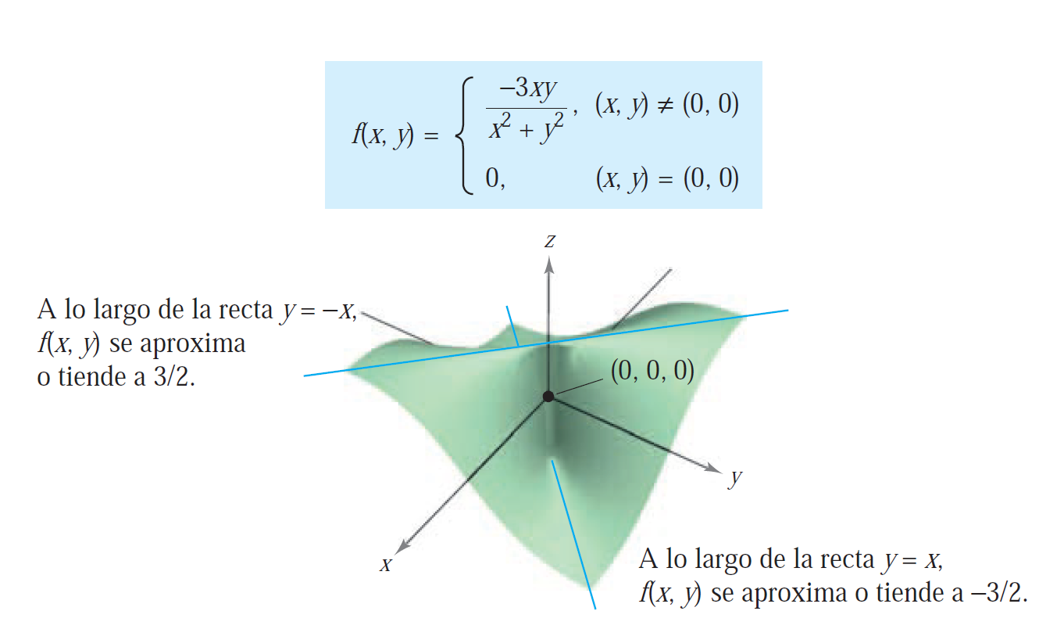
Consideramos la función:

\[\begin{split} f(x,y)=\left\{ \begin{array}{ll} \dfrac{-3xy}{x^2+y^2} & \textrm{si }(x,y)\neq (0,0), \\ 0 & \textrm{si }(x,y)=(0,0). \end{array} \right. \end{split}\]

Veamos, en primer lugar, que tiene derivadas parciales en el origen:

\[\begin{eqnarray*} \dfrac{\partial f}{\partial x}(0,0)&=\lim_{h\to 0} \dfrac{f(h,0)-f(0,0)}{h}=\lim_{h\to 0}\dfrac{0-0}{h}=0,\\ \dfrac{\partial f}{\partial y}(0,0)&=\lim_{h\to 0} \dfrac{f(0,h)-f(0,0)}{h}=\lim_{h\to 0}\dfrac{0-0}{h}=0. \end{eqnarray*}\]

Sin embargo, es fácil comprobar que \(f\) no es continua en \((0,0)\). En efecto, si consideramos su límite restringido a la recta \(y=x\), obtenemos

\[\begin{split} \lim_{\substack{ (x,y)\to (0,0)\\ y=x}} f(x,y)=\lim_{x\to 0} f(x,x)=\lim_{x\to 0}\dfrac{-3x^2}{2x^2}=-\dfrac{3}{2}, \end{split}\]

mientras que considerando la recta \(y=-x\) se tiene

\[\begin{split} \lim_{\substack{ (x,y)\to (0,0)\\ y=-x}} f(x,y)=\lim_{x\to 0} f(x,-x)=\lim_{x\to 0}\dfrac{3x^2}{2x^2}=\dfrac{3}{2}. \end{split}\]

Como los dos resultados son distintos, concluimos que \(f\) no es continua en \((0,0)\).

Ahora podríamos comprobar que las únicas derivadas direccionales que existen son las dos derivadas parciales, pero eso os lo vamos a dejar como ejercicio y nos centraremos en un caso particular (y más sencillo): no existe la derivada en la dirección de \(\mathbf{u}=\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\).

\[\begin{eqnarray*} D_{\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)}f(0,0) &:=& \lim_{h\to 0}\frac{f\left( (0,0) + h\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right) \right)-f(0,0)}{h} \\ &=& \lim_{h\to 0}\frac{f\left(\frac{h}{\sqrt{2}},\frac{h}{\sqrt{2}}\right)}{h}=\lim_{h\to 0}\frac{\frac{-\frac{3h^2}{2}}{\frac{h^2}{2}+\frac{h^2}{2}}}{h}= \left\{\begin{array}{l}\displaystyle\lim_{h\to 0^-}\frac{-3}{2h}=\infty\\ \displaystyle\lim_{h\to 0^+}\frac{-3}{2h}=-\infty\end{array} \right. \end{eqnarray*}\]

¡Veamos estos límites con la ayuda de Sympy!

import sympy as sp

x, y, h = sp.symbols('x y h', real=True) 
f = sp.Lambda((x,y),-3*x*y/(x**2+y**2)) # Función f en puntos distintos del origen

print('Límite restringido a y=x: ', sp.limit(f(x,x),x,0) )
print('Límite restringido a y=-x: ', sp.limit(f(x,-x),x,0) )
print('Derivada parcial respecto a x en el (0,0): ', sp.limit((f(h,0)-0)/h,h,0) )
print('Derivada parcial respecto a y en el (0,0): ', sp.limit((f(0,h)-0)/h,h,0) )
print('Derivada en (0,0) en la dirección de y=x. Izda.: ', 
      sp.limit((f(h/sp.sqrt(2),h/sp.sqrt(2))-0)/h,h,0,dir='-') )
print('Derivada en (0,0) en la dirección de y=x. Dcha.: ', 
      sp.limit((f(h/sp.sqrt(2),h/sp.sqrt(2))-0)/h,h,0,dir='+') )

Límite restringido a y=x:  -3/2
Límite restringido a y=-x:  3/2
Derivada parcial respecto a x en el (0,0):  0
Derivada parcial respecto a y en el (0,0):  0
Derivada en (0,0) en la dirección de y=x. Izda.:  oo
Derivada en (0,0) en la dirección de y=x. Dcha.:  -oo

En resumen: como ya nos podíamos imaginar, después de todo lo que aprendimos en el cálculo de límites para funciones de dos variables, no es suficiente con estudiar las derivadas parciales. Necesitamos algo más.

Ese algo más es el concepto de diferenciabilidad, que está relacionado con la existencia de una aproximación lineal de la función en las proximidades del punto en cuestión.

Vamos a introducir, a continuación, su definición formal para el caso de funciones escalares de dos variables, resultando natural su extensión a más variables.

Definition (Diferenciabilidad)

Sea \(f:R\subset \mathbb{R}^2\longrightarrow \mathbb{R}\) con \(R\) abierto. Decimos que \(f\) es diferenciable en \((x_0,y_0)\in R\), si existen las derivadas parciales primeras de \(f\) en el punto \((x_0,y_0)\), y además

\[ \lim_{(x,y)\to (x_0,y_0)}\dfrac{f(x,y)- \Big( f(x_0,y_0)+\nabla f(x_0,y_0)\cdot (x-x_0,y-y_0) \Big)}{\left\|(x-x_0,y-y_0)\right\|}=0. \]

Decimos que \(f\) es diferenciable en \(R\), si lo es en cada punto de \(R\).

A continuación, vamos a analizar este límite, con la ayuda de la librería Sympy, para comprobar que la función del ejemplo anterior no es diferenciable en el \((0,0)\).

Fíjate en que, por un lado estamos considerando \((x_0,y_0)=(0,0)\) y, por otra, ya vimos que \(\frac{\partial f}{\partial x} (0,0) = \frac{\partial f}{\partial y} (0,0) = 0\), por lo que \(\nabla f(x_0,y_0) = \nabla f(0,0) = (0, \; 0)\). De aquí que

\[\begin{eqnarray*} && \lim_{(x,y)\to (0,0)}\dfrac{f(x,y)- \Big( f(0,0)+ \nabla f(0,0) \cdot (x-0,y-0) \Big)}{\left\|(x-0,y-0)\right\|} \\ &=& \lim_{(x,y)\to (0,0)}\dfrac{f(x,y)}{\left\|(x,y)\right\|} = \lim_{(x,y)\to (0,0)}\dfrac{-3xy}{\left(x^2+y^2\right)\sqrt{x^2+y^2}}. \end{eqnarray*}\]

Y al hacer este límite, por rectas, obtendremos como resultado \(+\) o \(-\infty\), como nos confirma Sympy (al ser distinto de \(0\), \(f\) no es diferenciable en \((0,0)\)):

import sympy as sp

x, y = sp.symbols('x y', real=True) 
f = sp.Lambda((x,y), -3*x*y/(x**2+y**2) ) 

# Ahora definimos fun = f entre ||(x,y)|| 
fun = sp.Lambda((x,y), f(x,y)/sp.sqrt(x**2+y**2) )  

# calculamos el límite a través de rectas
m = sp.Symbol('m', real=True)
print('Límites direccionales: ', sp.limit(fun(x,m*x),x,0) )

Límites direccionales:  -oo*sign(m)

3.3.2. Propiedades para funciones diferenciables

Finalizamos la sección estableciendo dos condiciones para la diferenciabilidad: la necesaria de continuidad y la suficiente de continuidad de las derivadas parciales.

Theorem (Diferenciabilidad implica continuidad )

Si \(f\) es diferenciable en \(\mathbf{x}_0\), entonces \(f\) es continua en \(\mathbf{x}_0\).

Theorem (Condición suficiente para la diferenciabilidad )

Si las derivadas parciales (de primer orden) de \(f\) son continuas en una región abierta \(R\), entonces \(f\) es diferenciable en \(R\).