1.3. El producto escalar

En las dos secciones precedentes hemos introducido dos operaciones para vectores: la suma y el producto por un escalar. Ahora vamos a estudiar una tercera operación: el producto escalar.

1.3.1. Producto escalar. Definición y propiedades

Definition (Producto escalar)

El producto escalar es una aplicación \(\mathbb{R}^{n} \times \mathbb{R}^{n} \to \mathbb{R}\) que se define, en general, como

\[ \mathbf{u}\cdot\mathbf{v} := \sum_{i=1}^{n} u_{i} v_{i} \in \mathbb{R}. \]

Así, en los casos que venimos estudiando,

1. En \(\mathbb{R}^{2}\), \(\displaystyle \mathbf{u} \cdot \mathbf{v} = u_{1}v_{1} + u_{2}v_{2} \in \mathbb{R}\).

2. En \(\mathbb{R}^{3}\), \(\displaystyle \mathbf{u} \cdot \mathbf{v} = u_{1}v_{1} + u_{2}v_{2} + u_{3}v_{3} \in \mathbb{R}\).

Example

• El producto escalar de los vectores en el plano \(\mathbf{u} = (1,2)\) y \(\mathbf{v} = (-3,4)\) es:

  \[ \mathbf{u}\cdot\mathbf{v} = 1 \, (-3) + 2* 4 = -3 + 8 = 5.\]

• El producto escalar de los vectores en el espacio \(\mathbf{u} = (1,2,3)\) y \(\mathbf{v} = (-3,4,-5)\) es:

  \[ \mathbf{u}\cdot\mathbf{v} = 1 \, (-3) + 2* 4 + 3 \, (-5)= -3 + 8 -15 = -10.\]

Property

Sean \(\mathbf{u}\), \(\mathbf{v}\) y \(\mathbf{v}\) vectores en \(\mathbb{R}^{n}\) y \(c\in\mathbb{R}\). Entonces

1. \(\mathbf{u}\cdot\mathbf{v} = \mathbf{v}\cdot\mathbf{u}\) (propiedad conmutativa).

2. \(\mathbf{u}\cdot(\mathbf{v}+\mathbf{w}) = \mathbf{u}\cdot\mathbf{v} + \mathbf{u}\cdot\mathbf{w}\) (propiedad distributiva).

3. \(c\, (\mathbf{u}\cdot\mathbf{v}) = c\, \mathbf{u}\cdot \mathbf{v} = \mathbf{u}\cdot c\, \mathbf{v}\).

4. \(\mathbf{0}\cdot\mathbf{v} = \mathbf{0}\).

5. \(\mathbf{u}\cdot\mathbf{u} = \|\mathbf{u}\|^2\).

Nota: En Numpy se calcula con el comando np.dot (que también admite la sintaxis, para los vectores u y v, u.dot(v)):

import numpy as np

# Definimos los vectores u y v
u = np.array([1, 2, 3])
v = np.array([-3, 4, -5])

# Calculamos el producto escalar de u y v con np.dot
dot_product = np.dot (u,v)
print('Producto escalar de u y v: ', dot_product)

# Una opción equivalente de llamar a la misma función np.dot:
dot_product = u.dot(v)
print('Producto escalar de u y v: ', dot_product)

Producto escalar de u y v:  -10
Producto escalar de u y v:  -10

Para hacer el producto escalar en Sympy tenemos que usar la segunda sintaxis. Recuerda que en este caso los vectores tienen que definirse como sp.Matrix.

import sympy as sp

u = sp.Matrix([sp.frac('1/2'), sp.frac('1/3'), 1])
v = sp.Matrix([sp.frac('1/5'), 1, 2])

# Calculamos el producto escalar de u y v en Sympy
product = u.dot(v)
print(product)

73/30

1.3.2. Ángulo entre dos vectores

El ángulo entre dos vectores, \(\mathbf{u}\), \(\mathbf{v}\in\mathbb{R}^{2}\), ambos distintos de \(\mathbf{0}\), es el ángulo \(\theta\), \(\theta\in [0,\pi]\), entre estos vectores situados en su posición estándar (es decir, con el punto inicial de ambos en el origen de coordenadas).

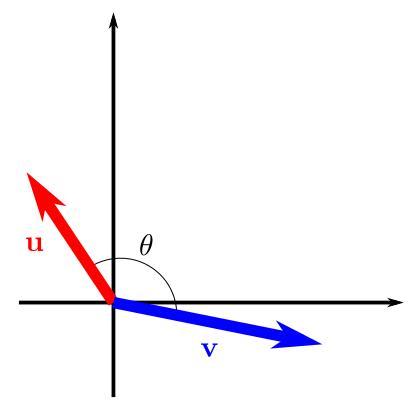
Puede calcularse utilizando la siguiente propiedad:

Property

Si \(\theta\) es el ángulo entre los vectores \(\mathbf{u}\), \(\mathbf{v}\in\mathbb{R}^{2}\), ambos distintos de \(\mathbf{0}\), entonces

\[ \cos\theta = \frac{\mathbf{u}\cdot\mathbf{v}}{\|\mathbf{u}\|\|\mathbf{v}\|}, \]

o, equivalentemente,

\[ \theta = \arccos\left(\frac{\mathbf{u}\cdot\mathbf{v}}{\|\mathbf{u}\|\|\mathbf{v}\|}\right), \]

Debemos hacer algunas consideraciones sobre esta propiedad:

1. Queremos destacar que, como el denominador en esta fracción es siempre un número positivo, \(\mathbf{u}\cdot\mathbf{v}\) y \(\cos\theta\) tendrán siempre el mismo signo. Por lo tanto podemos deducir fácilmente el signo de \(\mathbf{u}\cdot\mathbf{v}\) según el signo de \(\cos\theta\), como mostramos en la siguiente figura.

   

2. Dos vectores distintos a \(\mathbf{0}\) son perpendiculares si y sólo si su producto escalar es \(0\). En este caso se dice que estos dos vectores son ortogonales.

3. De la fórmula anterior, si se conoce el ángulo, \(\theta\), que forman dos vectores, se deduce una manera alternativa de calcular el producto escalar:

   \[ \mathbf{u}\cdot\mathbf{v} = \|\mathbf{u}\| \|\mathbf{v}\| \cos(\theta). \]

Vamos a hacer un ejercicio sencillo: calcularemos el ángulo que forman los vectores \(\mathbf{u} = (3,-1,2)\) y \(\mathbf{v} = (-4,0,2)\). Te sugerimos que después practiques tú, calculando los ángulos que forman cada uno de estos vectores con \(\mathbf{w} = (1,-2,-2)\).

Haremos, en primer lugar, los cálculos utilizando Sympy, paso a paso, tal como lo deberías hacer en papel. Luego realizaremos el mismo cálculo, aprovechando la mayor potencia numérica de Numpy.

import sympy as sp
# Definimos el vectores
u = Matrix([3, -1, 2])
v = Matrix([-4, 0, 2])

# Calculamos las normas de los vectores
norma_u = sp.sqrt(u.dot(u))
norma_v = sp.sqrt(v.dot(v))

# Calculamos el coseno del ángulo entre u y v
cos_theta = u.dot(v) / (norma_u*norma_v)
display('Coseno del ángulo entre los vectores: ',cos_theta)

# Finalmente, calculamos este ángulo utilizando la función arco-coseno:
theta = sp.acos(cos_theta)
display('Ángulo entre u y v: ', theta)

'Coseno del ángulo entre los vectores: '

\[\displaystyle - \frac{2 \sqrt{70}}{35}\]

'Ángulo entre u y v: '

\[\displaystyle \operatorname{acos}{\left(- \frac{2 \sqrt{70}}{35} \right)}\]

import numpy as np

# Definimos los vectores u y v
u = np.array([3, -1, 2])
v = np.array([-4, 0, 2])

# Calculamos y almacenamos las normas de estos vectores
norm_u = np.linalg.norm(u) 
norm_v = np.linalg.norm(v) 

# Ángulo entre u y v:
cos_theta1 = np.dot(u,v) / (norm_u * norm_v)
theta1 = np.arccos(cos_theta1)

display('Ángulo entre u y v: ', theta1)

'Ángulo entre u y v: '

2.0692767639323297

1.3.3. Cosenos directores

En general, nos va a convenir medir los ángulos que un vector dado, \(\mathbf{v}\), forma con los tres vectores canónicos, \(\mathbf{i}\), \(\mathbf{j}\) y \(\mathbf{k}\). Lo ilustramos con la siguiente figura, obtenida de la aplicación en Geogebra creada por Elvira Martínez, y con la que podéis jugar aquí: https://www.geogebra.org/m/PvPNNGb9.

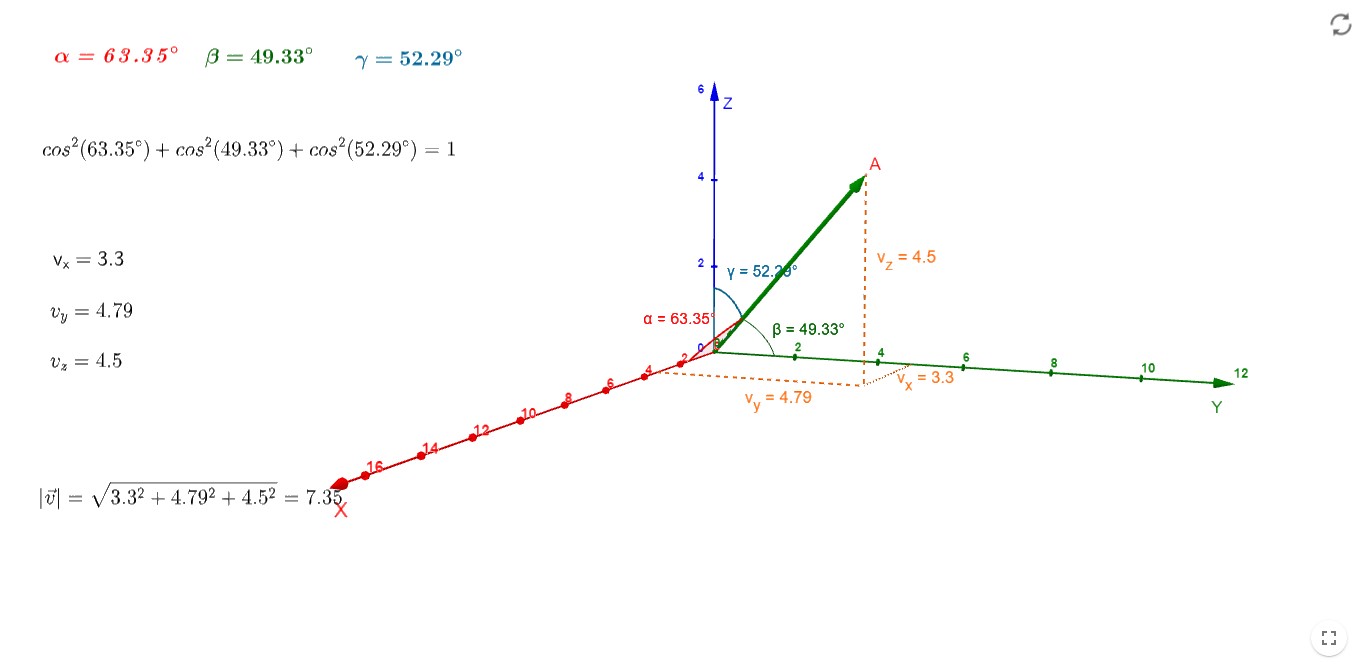
Definition (Ángulos y cosenos directores)

Dado un vector \(\mathbf{v} = \left(v_{1}, v_{2}, v_{3}\right)\neq \mathbf{0}\). Llamaremos ángulos directores a

• \(\alpha\), el ángulo que forma \(\mathbf{v}\) con el vector canónico \(\mathbf{i}\).

• \(\beta\), el ángulo que forma \(\mathbf{v}\) con el vector canónico \(\mathbf{j}\).

• \(\gamma\), el ángulo que forma \(\mathbf{v}\) con el vector canónico \(\mathbf{k}\).

Los cosenos de estos ángulos se llaman cosenos directores.

Podemos calcular los cosenos directores con la última propiedad enunciada:

• \(\cos\alpha = \dfrac{\mathbf{v}\cdot\mathbf{i}}{\|\mathbf{v}\|\|\mathbf{i}\|} = \dfrac{ v_{1} } {\|\mathbf{v}\|}\).

• \(\cos\beta = \dfrac{\mathbf{v}\cdot\mathbf{j}}{\|\mathbf{v}\|\|\mathbf{j}\|} = \dfrac{ v_{2} } {\|\mathbf{v}\|}\).

• \(\cos\gamma = \dfrac{\mathbf{v}\cdot\mathbf{k}}{\|\mathbf{v}\|\|\mathbf{k}\|} = \dfrac{ v_{3} } {\|\mathbf{v}\|}\).

Una consecuencia interesante de estas fórmulas es que los cosenos directores nos permiten escribir la forma normalizada de cualquier vector:

\[ \frac{\mathbf{v}} {\|\mathbf{v}\|} = \frac{ v_{1} } {\|\mathbf{v}\|} \mathbf{i} + \frac{ v_{2} } {\|\mathbf{v}\|} \mathbf{j} + \frac{ v_{3} } {\|\mathbf{v}\|} \mathbf{k} = \cos\alpha \mathbf{i} + \cos\beta \mathbf{j} + \cos\gamma \mathbf{k}. \]

Como ejercicio te proponemos que calcules, a mano, con Sympy y, finalmente, con Numpy, los ángulos y cosenos directores para el vector \(\mathbf{v} = (2,3,4)\).

1.3.4. Proyecciones y componentes vectoriales

Vamos a ver ahora una especie de operación inversa para la suma de vectores. Aprenderemos a calcular las descomponer un vector en función de otros dos o tres (en función de que nos movamos en el plano o en el espacio 3D) vectores.

Esta operación, que, en principio suena rara, es muy habitual en muchas aplicaciones físicas. Tal vez el ejemplo más habitual sea el de descomponer la fuerza de la gravedad sobre un peso situado en un plano inclinado en sus componentes horizontal y vertical, como se muestra en el siguiente dibujo (imagen obtenida de la aplicación de Geogebra de Jesús Benayas Yepes, https://www.geogebra.org/m/fwBuf7Hy):

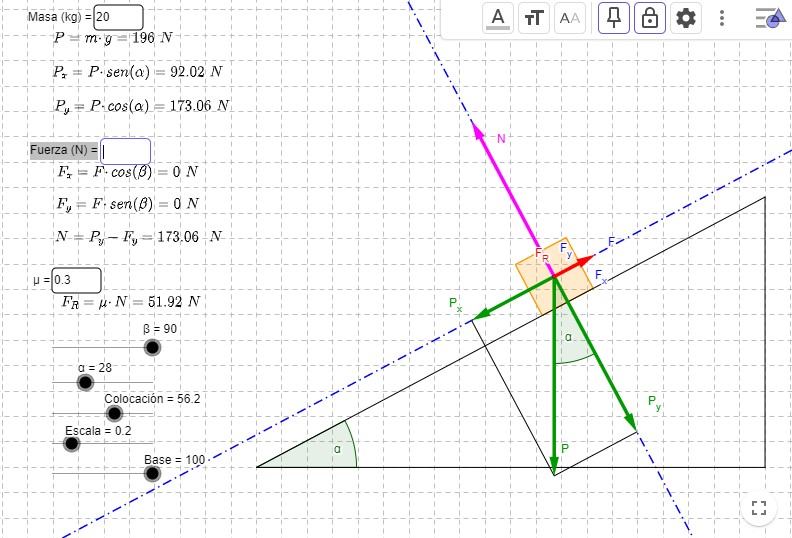
Definition (Proyecciones)

Consideramos dos vectores arbitrarios, \(\mathbf{u}\) y \(\mathbf{v}\), distintos de \(\mathbf{0}\). Entonces:

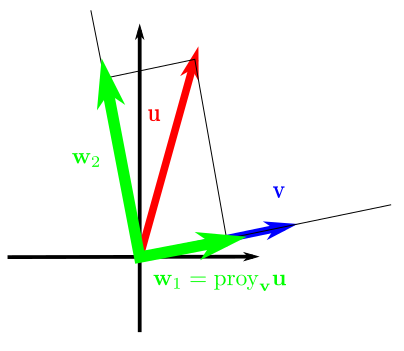
• Definimos la proyección de \(\mathbf{u}\) en la dirección de \(\mathbf{v}\) como el vector

  \[ \mathbf{w}_{1} \equiv \mathrm{proy}_{\mathbf{v}} \mathbf{u} = \left(\frac{ \mathbf{u}\cdot\mathbf{v} }{ \|\mathbf{v}\|^2 }\right) \mathbf{v}. \]

• Definimos la componente vectorial de \(\mathbf{u}\) ortogonal a \(\mathbf{v}\) como el vector

  \[ \mathbf{w}_{2} = \mathbf{u} - \mathbf{w}_{1} = \mathbf{u} - \mathrm{proy}_{\mathbf{v}} \mathbf{u}. \]

Con esta definición, podemos escribir \(\mathbf{u} = \mathbf{w}_{1} + \mathbf{w}_{2}\), siendo \(\mathbf{w}_{1}\) paralelo a \(\mathbf{v}\) y \(\mathbf{w}_{2}\) ortogonal a \(\mathbf{v}\).

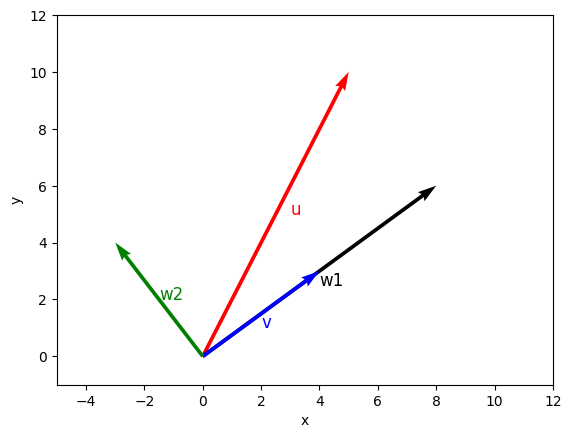
A continuación, como ejemplo, vamos a calcular con Numpy y a dibujar con Matplotlib las proyecciones de \(\mathbf{u} = (5,10)\) respecto a \(\mathbf{v}=(4,3)\). ¡Anímate a hacerlo a mano!

import numpy as np
import matplotlib as mp
import matplotlib.pyplot as plt

# Definimos los vectores u y v
u = np.array([5, 10])
v = np.array([4, 3])

# Calculamos las proyecciones de u respecto a v
w1 = ( np.dot(u,v)/ np.linalg.norm(v)**2 ) * v
w2 = u - w1 

# Ahora dibujamos estos vectores
plt.quiver(np.array([0,0,0,0]), np.array([0,0,0,0]), np.array([u[0],w1[0],v[0],w2[0]]), np.array([u[1],w1[1],v[1],w2[1]]), color=['r','k','b','g'], angles='xy', scale_units='xy', scale=1)

# Definición de los límites de los ejes
plt.xlim([-5,12])
plt.ylim([-1,12])

# Etiquetas de los ejes
plt.xlabel('x')
plt.ylabel('y')

# Añadimos etiquetas a los vectores
plt.text(u[0]/2+0.5, u[1]/2, 'u', fontsize=12, color='r')
plt.text(v[0]/2, v[1]/2-0.5, 'v', fontsize=12, color='b')
plt.text(w1[0]/2, w1[1]/2-0.5, 'w1', fontsize=12, color='k')
plt.text(w2[0]/2, w2[1]/2, 'w2', fontsize=12, color='g')

# Visualización
plt.show()