Derivación con Python
Contents
5.5. Derivación con Python#
Esta sección pretende ser un compendio (esperemos que claro y ordenado) de todo el Python
que hemos ido usando en las cinco primeras secciones del Capítulo 3.
Objetivos:
Cálculo de las derivadas parciales y direccionales.
Cálculo del vector gradiente.
Cálculo del plano tangente y de la recta normal.
Regla de la cadena.
5.5.1. Derivadas parciales para funciones de dos variables con Python#
Veamos ahora cómo calcular derivadas parciales utilizando sympy.
La función clave es sp.diff. que debe llevar como argumentos la expresión a derivar (o función Lambda, también vale) y, a continuación, la variable respecto a la que queremos hacerlo.
Veamos un par de ejemplos:
import sympy as sp
x, y = sp.symbols('x y', real=True) # define las variables simbólicas x, y
f_expr = 5* x**3 * y**2 + 4* x**2 * y**3
df_x_expr = sp.diff(f_expr,x) # Derivada parcial respecto a x
df_y_expr = sp.diff(f_expr,y) # Derivada parcial respecto a y
df_x = sp.Lambda((x,y),df_x_expr) # Creamos una función Lambda para la derivada respecto x
display(df_x_expr)
display(df_y_expr)
print("df_x(1,2): ",df_x(1,2)) # Usamos la función Lambda para evaluar la derivada en un punto
display(df_x)
\[\displaystyle 15 x^{2} y^{2} + 8 x y^{3}\]
\[\displaystyle 10 x^{3} y + 12 x^{2} y^{2}\]
df_x(1,2): 124
\[\displaystyle \left( \left( x, \ y\right) \mapsto 15 x^{2} y^{2} + 8 x y^{3} \right)\]
5.5.2. Derivadas parciales para funciones de tres o más variables#
import sympy as sp
x, y, z = sp.symbols('x y z', real=True) # define las variables simbólicas x, y, z
f_expr = 5* x**4 * y**3 * z**2 + 4* x**2 * y**3 * z**4
df_x_expr = sp.diff(f_expr,x) # Derivada parcial respecto a x
df_y_expr = sp.diff(f_expr,y) # Derivada parcial respecto a y
df_z_expr = sp.diff(f_expr,z) # Derivada parcial respecto a z
df_x = sp.Lambda((x,y,z),df_x_expr) # Creamos una función Lambda para la derivada respecto x
display(df_x_expr)
display(df_y_expr)
display(df_z_expr)
print("df_x(1,2,3): ",df_x(1,2,3)) # Usamos la función Lambda para evaluar la derivada en un punto
display(df_x)
\[\displaystyle 20 x^{3} y^{3} z^{2} + 8 x y^{3} z^{4}\]
\[\displaystyle 15 x^{4} y^{2} z^{2} + 12 x^{2} y^{2} z^{4}\]
\[\displaystyle 10 x^{4} y^{3} z + 16 x^{2} y^{3} z^{3}\]
df_x(1,2,3): 6624
\[\displaystyle \left( \left( x, \ y, \ z\right) \mapsto 20 x^{3} y^{3} z^{2} + 8 x y^{3} z^{4} \right)\]
5.5.3. Derivadas parciales de orden superior#
import sympy as sp
x, y = sp.symbols('x y', real=True) # define las variables simbólicas x, y
f_expr = 5* x**3 * y**2 + 4* x**2 * y**3
df_xx_expr = sp.diff(f_expr,x,x) # Derivada parcial respecto a x dos veces. También se puede escribir sp.diff(f_expr,x,2)
df_yx_expr = sp.diff(f_expr,x,y) # Derivada parcial primero respecto x, luego respecto y
df_xy_expr = sp.diff(f_expr,y,x) # Derivada parcial primero respecto y, luego respecto x
df_yy_expr = sp.diff(f_expr,y,y) # Derivada parcial respecto a x dos veces
display(df_xx_expr)
display(df_yx_expr)
display(df_xy_expr)
display(df_yy_expr)
\[\displaystyle 2 y^{2} \cdot \left(15 x + 4 y\right)\]
\[\displaystyle 6 x y \left(5 x + 4 y\right)\]
\[\displaystyle 6 x y \left(5 x + 4 y\right)\]
\[\displaystyle 2 x^{2} \cdot \left(5 x + 12 y\right)\]
5.5.4. Cálculo del vector gradiente#
Calculamos el vector gradiente como la transpuesta de la matriz jacobiana para funciones de \(\mathbb{R}^{n}\) a \(\mathbb{R}\), como se muestra en el siguiente ejemplo.
import sympy as sp
x, y = sp.symbols('x y', real=True)
F = sp.Matrix([3*x**2-5*y**2])
# Cálculo del jacobiano de F
jac_F = F.jacobian([x,y])
grad_F = jac_F.transpose()
# NOTA: Se puede hacer lo mismo en un único paso:
# grad_F = F.jacobian([x,y]).transpose()
display(grad_F)
\[\begin{split}\displaystyle \left[\begin{matrix}6 x\\- 10 y\end{matrix}\right]\end{split}\]
5.5.5. Derivada direccional#
Mostramos a continuación cómo calcular la derivada direccional de la función \(f(x,y) = x\sqrt{y}\), en un punto cualquiera \((x,y)\), según la dirección que marca el vector \(\mathbf{u}=(1,2)\).
import sympy as sp
x, y = sp.symbols('x y', real=True)
F = sp.Matrix([ x*sp.sqrt(y) ])
grad_F = F.jacobian([x,y]).transpose()
display(grad_F)
u = sp.Matrix([1, 2]) # Definimos un vector director unitario
display(u)
norm_u = sp.sqrt(u.dot(u))
u = u/norm_u
display(u)
df_u = u.dot(grad_F)
display(df_u)
\[\begin{split}\displaystyle \left[\begin{matrix}\sqrt{y}\\\frac{x}{2 \sqrt{y}}\end{matrix}\right]\end{split}\]
\[\begin{split}\displaystyle \left[\begin{matrix}1\\2\end{matrix}\right]\end{split}\]
\[\begin{split}\displaystyle \left[\begin{matrix}\frac{\sqrt{5}}{5}\\\frac{2 \sqrt{5}}{5}\end{matrix}\right]\end{split}\]
\[\displaystyle \frac{\sqrt{5} x}{5 \sqrt{y}} + \frac{\sqrt{5} \sqrt{y}}{5}\]
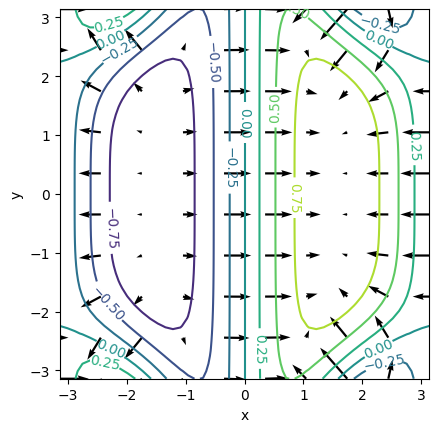
5.5.6. El vector gradiente es ortogonal a las curvas de nivel#
Lo mostramos gráficamente sobre un ejemplo sencillo.
import sympy as sp
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
x, y = sp.symbols('x y', real=True) # define las variables simbólicas x, y
F = sp.Matrix([ sp.sin(x)*sp.cos(x*y**2/10) ])
F_lamb = sp.lambdify((x,y),F[0,0], "numpy")
# display(F_lamb)
grad_F = F.jacobian([x,y]).transpose()
grad_F_lamb = sp.lambdify((x,y), [grad_F[0,0],grad_F[1,0]], "numpy")
# Creamos una función lambdify del gradiente para poder evaluarlo en cualquier punto
N = 50 # 50 puntos en cada dirección de los ejes cartesianos para las curvas de nivel
x = np.linspace(-np.pi, np.pi, N)
y = np.linspace(-np.pi, np.pi, N)
X, Y = np.meshgrid(x, y)
Values = F_lamb(X,Y)
Ng = 10 # 10 puntos en cada dirección de los ejes cartesianos para los vectores gradientes
xg = np.linspace(-np.pi, np.pi, Ng)
yg = np.linspace(-np.pi, np.pi, Ng)
Xg, Yg = np.meshgrid(xg, yg)
Values_Grad=grad_F_lamb(Xg,Yg)
p = plt.contour(X, Y, Values) # Representación gráfica de las curvas de nivel
plt.clabel(p) # Se añade el valor numérico a cada curva de nivel
plt.quiver(Xg, Yg, Values_Grad[0], Values_Grad[1]) # Representación gráfica del campo de vectores gradiente
# plt.quiver(Xg, Yg, Values_Grad) # Representación gráfica del campo de vectores gradiente
# Etiquetas de los ejes
plt.xlabel('x')
plt.ylabel('y')
plt.axis('square')
plt.show()
5.5.7. Cálculo y representación del plano tangente y de la recta normal con Python#
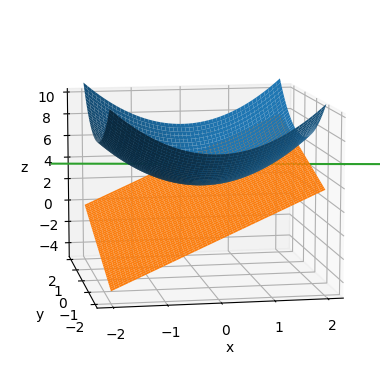
Consideramos a continuación el problema de encontrar el plano tangente y la recta normal a la superficie \(z=f(x,y)=x^2+y^2+3\) en el punto \((x_0,y_0,z_0)=(1,1/2,f(1,1/2))\), que resolvemos, en Python, aplicando los resultados expuestos. En primer lugar, importamos los módulos necesarios teniendo en cuenta que usaremos Matplotlib para la representación gráfica.
import sympy as sp
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
%matplotlib inline
Ahora vamos a calcular:
Plano tangente.
Ángulo de inclinación de éste.
Recta normal.
x, y, z, t = sp.symbols('x y z t', real=True) # definimos las variables simbólicas
f = sp.Lambda((x,y), x**2+y**2+3)
x0 = 1; y0=sp.Rational(1/2); z0=f(x0,y0)
# Cálculo de la ecuación del plano tangente
F = sp.Matrix([f(x,y)-z])
grad_F = F.jacobian([x,y,z]).transpose()
n = grad_F.subs(x,x0).subs(y,y0).subs(z,z0)
plano_tang = sp.solve(sp.Eq(n[0]*(x-x0)+n[1]*(y-y0)+n[2]*(z-z0),0),z)[0]
display(plano_tang)
# Cálculo de la inclinación del plano tangente
angulo=sp.acos(sp.Abs(n[2])/sp.sqrt(n.dot(n)))
display('Ángulo de inclinación del plano tangente:',angulo)
# Cálculo de la ecuación vectorial de la recta normal
recta_norm = sp.Lambda(t,(x0+t*n[0], y0+t*n[1], z0+t*n[2]))
display(recta_norm)
\[\displaystyle 2 x + y + \frac{7}{4}\]
'Ángulo de inclinación del plano tangente:'
\[\displaystyle \operatorname{acos}{\left(\frac{\sqrt{6}}{6} \right)}\]
\[\displaystyle \left( t \mapsto \left( 2 t + 1, \ t + \frac{1}{2}, \ \frac{17}{4} - t\right) \right)\]
Una vez calculado el plano tangente y la recta normal, se traslada la información del módulo Sympy a Numpy, para un uso posterior en Matplotlib y graficamos:
f_n = sp.lambdify((x,y),f(x,y),"numpy") # función numpy con la expresión de f(x,y)
Plano_tang = sp.lambdify((x,y),plano_tang,"numpy")
Recta_norm = sp.lambdify(t,recta_norm(t),"numpy")
# Nube de puntos para representar la superficie y el plano
N = 50
x = np.linspace(-2, 2, N)
y = np.linspace(-2, 2, N)
X, Y = np.meshgrid(x, y)
fval = f_n(X,Y)
Pval = Plano_tang(X,Y)
# Conjunto de puntos para representar la recta normal
tvec = np.linspace(-2, 2, 100)
Rval = Recta_norm(tvec)
# Creación de la figura 3D
fig = plt.figure()
ax = plt.axes(projection="3d")
# Representación de la superficie z=f(x,y), el plano tangente y la recta normal
surf_F = ax.plot_surface(X, Y, fval)
surf_Plano = ax.plot_surface(X, Y, Pval)
recta = ax.plot3D(*Rval)
# Etiquetas de los ejes
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
# Punto de vista del observador: elevación, ángulo azimutal
ax.view_init(elev=10, azim=-100)
ax.auto_scale_xyz([-2,2],[-2,2],[-5,10])
plt.show()
