3.6. Extremos relativos#

3.6.1. Definición de extremo relativo#

Antes de nada, para poneros al día y recordar lo que os enseñaron (esperamos) en el instituto sobre máximos y mínimos relativos para funciones de una variable, os recomendamos la lectura de la sección de aplicaciones de la derivada en el JB de Cálculo en una variable.

Vamos a empezar esta sección definiendo lo que es un mínimo y un máximo relativo.

Definition (Máximo y mínimo relativo )

Sea \(f:\mathcal{D}\subset\mathbb{R}^{2} \to \mathbb{R}\), \((x_{0},y_{0})\in \mathcal{D}\).

  1. Diremos que \(f\) tiene un máximo relativo en \((x_{0},y_{0})\) si

    \[ \exists\delta>0\text{ tal que } f(x_{0},y_{0})\geq f(x,y),\qquad \forall(x,y)\in D_\delta(x_0,y_0). \]

  2. Diremos que \(f\) tiene un mínimo relativo en \((x_{0},y_{0})\) si

    \[ \exists\delta>0\text{ tal que } f(x_{0},y_{0})\leq f(x,y),\qquad \forall(x,y)\in D_\delta(x_0,y_0). \]

Si pensamos en una excursión al campo, decir que estamos en un máximo relativo quiere decir que estamos en los alto de una montaña (localmente, estamos en el punto más alto)… no tiene por qué ser la montaña más alta de la cordillera.

Mostramos como ejemplo la siguiente función, con varios máximos relativos (por ejemplo, en el \((0,0)\)) y varios mínimos relativos (por ejemplo, en \((\pi,\pi)\)).

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm

def func_ondulante(x, y):
    return np.cos(x) * np.cos(y)*np.exp(x/5)

x = np.linspace(-1*np.pi, 3*np.pi, 100)
y = np.linspace(-1*np.pi, 3*np.pi, 100)
X, Y = np.meshgrid(x, y)
Z = func_ondulante(X, Y)

fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')

surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm)

# Etiquetas de los ejes
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

# Orientamos los ejes
ax.azim = 60
ax.elev = 30
plt.show()

3.6.2. Condición necesaria#

La pregunta clave es: ¿dónde pueden estar los extremos (máximos o mínimos) relativos? En toda la inmensidad de \(\mathbb{R}^{2}\), ¿dónde los buscamos? Pues aplicaremos la misma idea que para funciones de una variable: o bien donde no exista derivada, o bien donde esta derivada valga \(0\). Pues aquí lo mismo, pero con el gradiente.

Definition (Punto crítico )

Sea \(f:\mathcal{D}\subset\mathbb{R}^{2} \to \mathbb{R}\), \((x_{0},y_{0})\in \mathcal{D}\). Diremos que el punto \((x_{0},y_{0})\) es un punto crítico de \(f\) si se satisface una de las condiciones siguientes:

  1. \(\mathbf{\nabla}f(x_{0},y_{0}) = \mathbf{0}\).

  2. No existe una de las dos derivadas parciales, \(\not\exists\dfrac{\partial f}{\partial x}(x_{0},y_{0})\) o \(\not\exists\dfrac{\partial f}{\partial y}(x_{0},y_{0})\).

Fijémenos en la primera de estas condiciones: \(\mathbf{\nabla}f(x_{0},y_{0}) = \mathbf{0}\). Eso es equivalente a que el plano tangente sea horizontal (paralelo al plano \(XY\)), como mostramos en la siguiente figura:

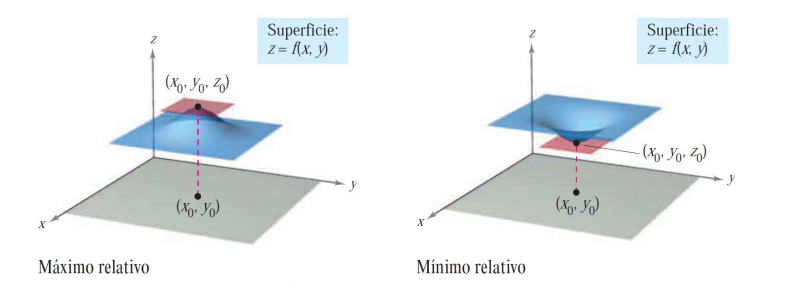
../../_images/3.6.Plano_tangente.png

La siguiente propiedad (condición necesaria) nos confirma dónde debemos buscar los máximos y mínimos relativos: en los puntos críticos (aunque no todos los puntos críticos serán extremos relativos).

Property (Condición necesaria para extremos relativos )

Sea \(f:D\subset\mathbb{R}^{2}\to\mathbb{R}\) y \(\left(x_{0},y_{0}\right)\) un punto en el interior de \(D\). Entonces, si \(\left(x_{0},y_{0}\right)\) es extremo relativo de \(f\), también tiene que ser punto crítico.

Dicho de manera esquemática

\[ \left(x_{0},y_{0}\right)\text{ extremo relativo de } f \Rightarrow \left(x_{0},y_{0}\right)\text{ punto crítico de } f \]

3.6.3. Criterio de la matriz hessiana#

Vale. Ya hemos encontrado los puntos críticos para una determinada función. ¿Y ahora? ¿Cómo sé si son máximos relativos, mínimos relativos o ninguna de las anteriores?

Pues recordemos lo que hacíamos en funciones de una variable: mirábamos el signo de la segunda derivada. Ahora vamos a hacer algo parecido… pero con cuidado, porque no hay una, sino cuatro derivadas segundas. Por lo tanto, lo primero que vamos a hacer es colocarlas en una matriz.

Definition (Matriz hessiana )

Sea \(f:\mathcal{D}\subset\mathbb{R}^{2} \to \mathbb{R}\), \((x_{0},y_{0})\in \mathcal{D}\). Supongamos que existen las cuatro derivadas parciales segundas de \(f\) en \((x_{0},y_{0})\). Definimos la matriz hessiana de \(f\) en \((x_{0},y_{0})\) como

\[\begin{split} \mathrm{Hess}f(x_{0},y_{0}) = \begin{bmatrix} \dfrac{\partial^{2} f}{\partial x^{2}} (x_{0}, y_{0}) & \dfrac{\partial^{2} f}{\partial x\partial y} (x_{0}, y_{0}) \\ \dfrac{\partial^{2} f}{\partial y \partial x} (x_{0}, y_{0}) & \dfrac{\partial^{2} f}{\partial y^{2}} (x_{0}, y_{0}) \end{bmatrix} \end{split}\]

Nota: La matriz hessiana recibe su nombre en honor al matemático alemán del siglo XIX Ludwig Otto Hesse y, en concreto, por las contribuciones que recoge en su libro Teoría de las superficies cuádricas generales, publicado en 1857.

Ahora ya podemos introducir la propiedad que nos permite clasificar los puntos críticos:

Property (Clasificación de puntos críticos )

Sea \(f:\mathcal{D}\subset\mathbb{R}^{2} \to \mathbb{R}\), \((x_{0},y_{0})\in \mathcal{D}\). Supongamos que se puede definir la matriz hessiana de \(f\) en \((x_{0},y_{0})\). Entonces:

  1. Si \(\det\mathrm{Hess}f(x_{0},y_{0}) > 0\) y \(\dfrac{\partial^{2} f}{\partial x^{2}} (x_{0}, y_{0}) < 0\), entonces \(f\) tiene en \((x_{0},y_{0})\) un máximo relativo.

  2. Si \(\det\mathrm{Hess}f(x_{0},y_{0}) > 0\) y \(\dfrac{\partial^{2} f}{\partial x^{2}} (x_{0}, y_{0}) > 0\), entonces \(f\) tiene en \((x_{0},y_{0})\) un mínimo relativo.

  3. Si \(\det\mathrm{Hess}f(x_{0},y_{0}) < 0\), entonces \(f\) tiene en \((x_{0},y_{0})\) un punto silla (es decir, un punto crítico que no es ni máximo ni mínimo relativo).

  4. Si \(\det\mathrm{Hess}f(x_{0},y_{0}) = 0\) el criterio no decide.

Nota: El nombre punto silla (o, mejor, punto de silla de montar, porque verás que la gráfica que viene a continuación no se parece nada a la silla en la que te vas a sentar para comer hoy) recibe su nombre del hiperboloide \(f(x,y) = y^2 - x^2\), que tiene en el \((0,0)\) un punto de estos.

import numpy as np
import sympy as sp
import matplotlib as mp
import matplotlib.pyplot as plt
from matplotlib import cm
%matplotlib notebook

x, y = sp.symbols('x y', real=True) 

f = sp.Lambda( (x,y) , y**2 - x**2 ) # definimos la función
fn= sp.lambdify( (x,y) , f(x,y) , "numpy" ) # función numpy de f

# Inicialización de la representación 3D
fig = plt.figure()
ax = plt.axes(projection="3d")

xx = np.linspace(-1, 1, 1000)
yy = np.linspace(-1, 1, 1000)
X, Y = np.meshgrid(xx, yy)
Z = fn(X,Y)

# Representación de la superficie
surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

# Orientamos los ejes
ax.azim = 20
ax.elev = 10

plt.show()

3.6.4. Extremos relativos con Python#

Vamos a continuación a mostrar, sobre un ejemplo, cómo se localizan los puntos críticos y como se clasifican, con la ayuda de Python.

Buscamos los puntos críticos de la función \(f(x,y) = -x^3 + 4xy - 2y^2 +1\) en todo \(\mathbb{R}^2\).

Lo vamos a hacer de una manera un tanto pedestre, pero te planteamos un reto: escribe una function que clasifique automáticamente los puntos críticos.

import sympy as sp
import numpy as np

x, y = sp.symbols('x y', real=True) # define as variables simbólicas x e y
f = sp.Lambda((x,y), -x**3 +4*x*y-2*y**2+1)

# Calculamos el gradiente de f
grad_f =  sp.transpose(sp.Matrix([f(x,y)]).jacobian([x,y]))
display(grad_f)

# Buscamos los puntos críticos
sol = sp.solve((sp.Eq(grad_f[0],0),sp.Eq(grad_f[1],0)),(x,y), dict=True)
display('Puntos críticos:', sol)

# Definimos la hessiana son sp.hessian
H = sp.Lambda((x,y), sp.hessian(f(x,y), (x,y)))
display('Matriz hessiana en (x,y): ', H(x,y))

# Clasificación del primer punto crítico
H0 = H(sol[0][x],sol[0][y])
display('Hessiana del primer punto crítico: ', H0)
print("Determinante: ",sp.det(H0), ". Posición (1,1):", H0[0,0])

# Clasificación del segundo punto crítico
H1 = H(sol[1][x],sol[1][y])
display('Hessiana del segundo punto crítico: ', H1)
print("Determinante: ",sp.det(H1), ". Posición (1,1):", H1[0,0])
\[\begin{split}\displaystyle \left[\begin{matrix}- 3 x^{2} + 4 y\\4 x - 4 y\end{matrix}\right]\end{split}\]
'Puntos críticos:'

[{x: 0, y: 0}, {x: 4/3, y: 4/3}]

'Matriz hessiana en (x,y): '
\[\begin{split}\displaystyle \left[\begin{matrix}- 6 x & 4\\4 & -4\end{matrix}\right]\end{split}\]
'Hessiana del primer punto crítico: '
\[\begin{split}\displaystyle \left[\begin{matrix}0 & 4\\4 & -4\end{matrix}\right]\end{split}\]
Determinante:  -16 . Posición (1,1): 0

'Hessiana del segundo punto crítico: '
\[\begin{split}\displaystyle \left[\begin{matrix}-8 & 4\\4 & -4\end{matrix}\right]\end{split}\]
Determinante:  16 . Posición (1,1): -8

# Vamos a dibujar esta función
import matplotlib as mp
import matplotlib.pyplot as plt
from matplotlib import cm
%matplotlib notebook

# Inicialización de la representación 3D
fig = plt.figure()
ax = plt.axes(projection="3d")
fn= sp.lambdify( (x,y) , f(x,y) , "numpy" ) # función numpy de f

# Creación de la nube de puntos (50 puntos en cada eje, x e y) 
xx = np.linspace(-1, 2, 1000)
yy = np.linspace(-1, 2, 1000)
X, Y = np.meshgrid(xx, yy)
Z = fn(X,Y)

# Representación de la superficie
surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm)
# Etiquetas de los ejes
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

# Orientamos los ejes
ax.azim = 5
ax.elev = 10

plt.show()