4.4. Cambio de variable#

Antes de empezar esta sección, te recomendamos que pongas al día tus conocimientos para funciones de una variable. Puedes consultar:

4.4.1. Matriz jacobiana y cambio de variable#

El método de cambio de variable esencialmente revierte la regla de la cadena para derivadas. En otras palabras, nos ayuda a integrar composición de funciones. A menudo, este método es útil para reducir la complejidad del cálculo de algunas integrales. Hay muchos casos en los que con las variables iniciales no sabremos resolver la integral, ya sea por la función a integrar, o por la complejidad de la expresión de los intervalos de integración. En estos casos, buscaremos cambios de variables que nos faciliten la resolución de la integral.

Theorem (Cambio de variable en integrales dobles)

Sea \(R\) una región en el plano \(XY\) y sea \(S\) una región en el plano \(UV\). Sean \(\mathbf{F}: S \subset \mathbb{R}^2 \rightarrow \mathbb{R}^2\) y \(G: R \subset \mathbb{R}^2 \rightarrow \mathbb{R}\) dos funciones tales que \(\mathbf{F}\) es inyectiva y \(\mathbf{F}(u,v) = (F_1(u,v),F_2(u,v)) \subset R\), donde \(F_1\) y \(F_2\) tienen primeras derivadas parciales continuas. Si \(G\) es continua en \(R\) y \(\det \mathrm{J}\mathbf{F}(u,v) \neq 0\) en \(S\), entonces

\[ \displaystyle \int_{R} \int G(x,y) \, dx \, dy = \int_{S} \int (G \circ \mathbf{F})(u,v) |\det \mathrm{J}\mathbf{F}(u,v)| \, du \, dv, \]

donde \(\mathrm{J}\mathbf{F}\) es la matriz jacobiana de \(\mathbf{F}\).

Example

Sea \(R\) la región delimitada por las líneas

\[ x - 2y = 0, \quad x - 2y = -4, \quad x + y = 4, \quad x + y = 1. \]
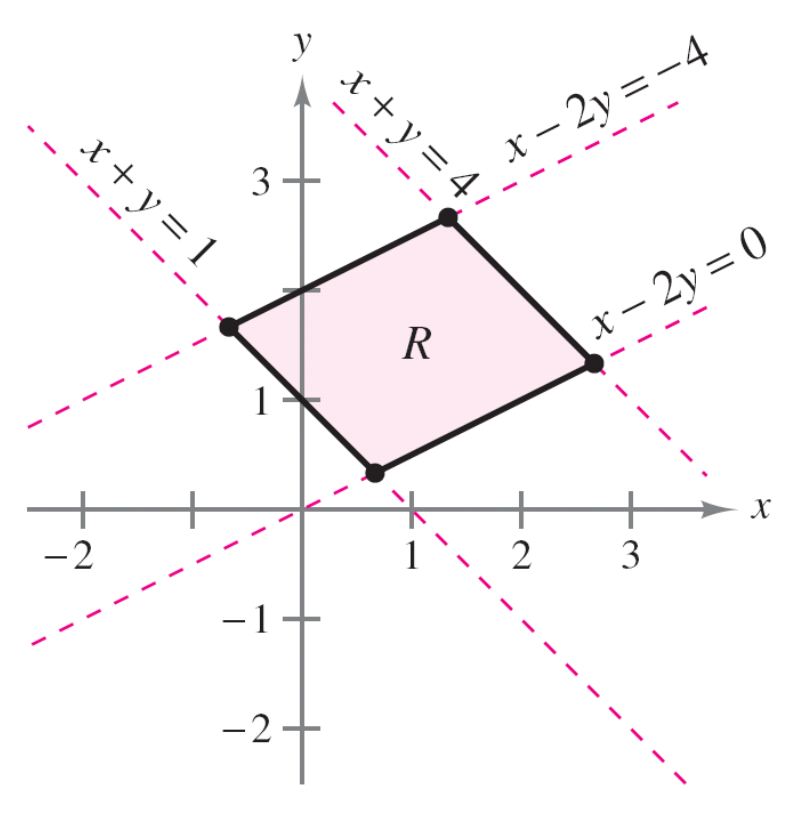
../../_images/5.4_Ejemplo_1.png

Evalúa la integral

\[ \displaystyle \int_R \int 9xy \, dA. \]

Solución:

Como es complejo establecer los intervalos de integración sobre \(R\), vamos a definir una región \(S\) más sencilla. Para ello, consideramos el siguiente cambio de variable:

\[\begin{split} \left\{\begin{array}{lcl} u &=& x + y \\ v &=& x - 2y \end{array}\right. \end{split}\]

Ahora sí, fácilmente podemos deducir los intervalos de integración de las nuevas variables a partir de la nueva región \(S = \Big{\{}(u,v) \in \mathbb{R}^2 \Big{/} 1 \le u \le 4, -4 \le v \le 0\Big{\}}\). Además, despejando \(x\) e \(y\) a partir del cambio de variable propuesto, obtenemos la función \(\mathbf{F}: S \subset \mathbb{R}^2 \rightarrow \mathbb{R}^2\) tal que

\[ \mathbf{F}(u,v) = \left(\frac{1}{3}(2u + v),\frac{1}{3}(u - v)\right). \]

Como

\[\begin{split} \det\mathrm{J}\mathbf{F}(u,v) = \begin{vmatrix} \frac{2}{3} & \frac{1}{3}\\ \frac{1}{3} & -\frac{1}{3} \end{vmatrix} = -\frac{1}{3}, \end{split}\]

por el resultado teórico anterior, obtenemos

\[\begin{equation*} \begin{split} \displaystyle \int_{R} \int 9xy \, dA & = \int_{S} \int 9 \left[\frac{1}{3}(2u + v)\frac{1}{3}(u - v)\right] \left|-\frac{1}{3}\right| \, dv \, du \\ & = \int_1^4 \int_{-4}^0 \frac{1}{3} (2u^2 - uv - v^2) \, dv \, du \\ & = \frac{1}{3} \int_1^4 \left[2u^2v - \frac{uv^2}{2} - \frac{v^3}{3}\right]_{-4}^0 \, du \\ & = \frac{1}{3} \int_1^4 \left(8u^2 + 8u - \frac{64}{3}\right) \, du \\ & = \frac{1}{3} \left[\frac{8u^3}{3} + 4u^2 - \frac{64}{3}u\right]_1^4 \\ & = \frac{164}{3}. \end{split} \end{equation*}\]

Podemos usar Sympy para que nos confirme lo bien que trabajamos:

import sympy as sp

x, y, u, v = sp.symbols('x y u v', real=True) # define las variables simbólicas x, y, u, v

# Definimos las funciones F y G como matrices
F = sp.Matrix([ 1/3*(2*u+v), 1/3*(u-v) ])
G = sp.Matrix([ 9*x*y ])

# Definimos la nueva función a integrar 
GoF_expr = G.subs(x,1/3*(2*u+v)).subs(y,1/3*(u-v))

# Calculamos el determinante de la matriz jacobiana asociada a F
det_jac_F = sp.det( F.jacobian([u,v]) )
display(det_jac_F)

# Calculamos la integral sobre la nueva región de integración
res = sp.integrate(GoF_expr*abs(det_jac_F), (v, -4, 0), (u, 1, 4))
display('Valor de la integral: ')
display(sp.simplify(res[0]))
\[\displaystyle -0.333333333333333\]
'Valor de la integral: '
\[\displaystyle 54.6666666666667\]

4.4.2. Integrales dobles en coordenadas polares#

En \(\mathbb{R}^2\), si la función a integrar o la región de integración tienen alguna clase de simetría radial, a menudo resulta conveniente aplicar la transformación de coordenadas cartesianas a coordenadas polares.

Theorem (Cambio de variable a la forma polar)

Sea \(R\) una región en el plano \(XY\) y sea \(S\) una región en el plano \(r\theta\). Sean \(\mathbf{F}: S \subset \mathbb{R}^2 \rightarrow \mathbb{R}^2\) y \(G: R \subset \mathbb{R}^2 \rightarrow \mathbb{R}\) dos funciones tales que \(\mathbf{F}(r,\theta) = (r\cos(\theta),r\sin(\theta)) \subset R\). Si \(S = \{(r,\theta) \in \mathbb{R}^+ \times [0,2\pi] | \alpha \le \theta \le \beta, 0 \le g_1(\theta) \le r \le g_2(\theta)\}\), donde \(g_1\) y \(g_2\) son continuas en \([\alpha,\beta]\) y \(G\) es continua en \(R\), entonces

\[\begin{eqnarray*} \int_{R} \int G(x,y) \, dA &=& \int_S \int (G \circ \mathbf{F})(r,\theta) |\det \mathrm{J}\mathbf{F}(r,\theta)| \, dr \, d\theta \\ &=& \int_{\alpha}^{\beta} \int_{g_1(\theta)}^{g_2(\theta)} G(r\cos(\theta),r\sin(\theta)) r \, dr \, d\theta. \end{eqnarray*}\]

Fíjate que, en este caso, como la aplicación que define el cambio de variable es \(\mathbf{F}(r,\theta) = (r\cos(\theta),r\sin(\theta)) \subset R\), su matriz jacobiana será

\[\begin{split} F(r,\theta) = \begin{bmatrix} \cos\theta & -r\sin\theta \\ \sin\theta & r\cos\theta\end{bmatrix} \end{split}\]

y, por tanto, el valor absoluto del determinante de esta matriz será

\[ \left| \det\mathrm{J}\mathbf{F}(r,\theta) \right| = \left| r\cos^2\theta + r\sin^2\theta \right| = \left| r\right | = r. \]

Example

Sea \(R\) la región anular que se encuentra entre los dos círculos

\[\begin{split} \left\{\begin{array}{lcl} x^2 + y^2 &=& 1, \\ x^2 + y^2 &=& 5. \end{array}\right. \end{split}\]
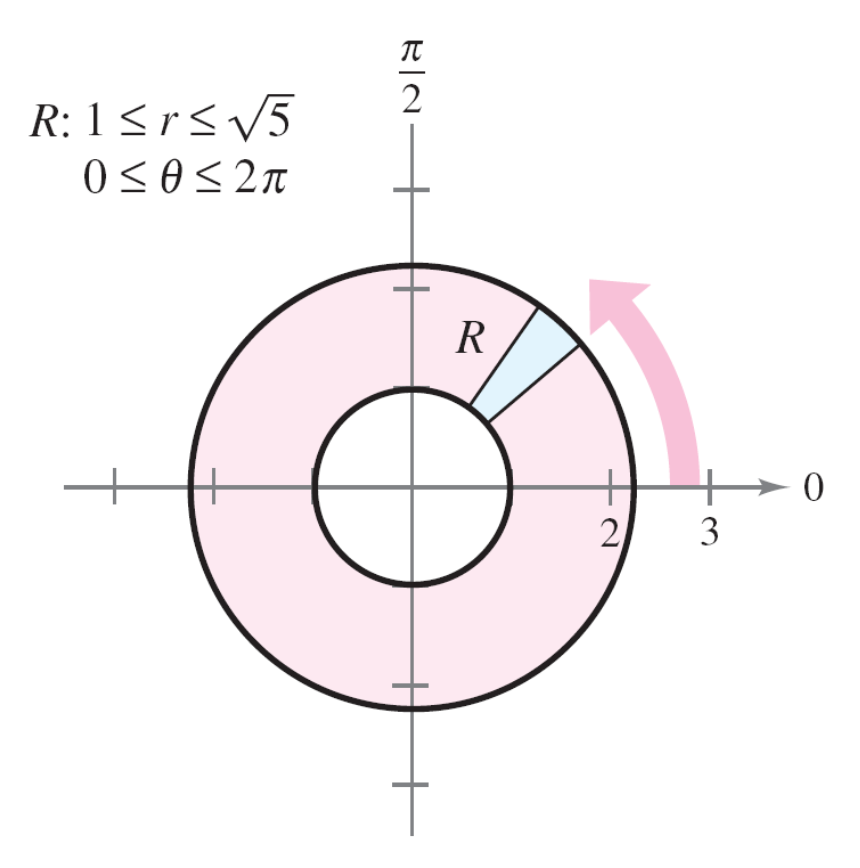
../../_images/5.4_Ejemplo_2.png

Evalúa la integral

\[ \displaystyle \int_R \int (x^2 + y) \, dA. \]

Solución:

Utilizando el cambio de variable a la forma polar, tenemos \(\mathbf{F}: S \subset \mathbb{R}^2 \rightarrow \mathbb{R}^2\)

\[ \mathbf{F}(u,v) = (r\cos(\theta),r\sin(\theta)), \]

donde los intervalos de integración de las nuevas variables son:

\[ 0 \le \theta \le 2\pi \quad \text{ y } \quad 1 \le r \le \sqrt{5}. \]

Por el resultado teórico anterior, obtenemos

\[\begin{equation*} \begin{split} \displaystyle \int_{R} \int (x^2 + y) \, dA & = \int_0^{2\pi} \int_{1}^{\sqrt{5}} (r^2\cos^2(\theta) + r\sin(\theta))r \, dr \, d\theta \\ & = \int_0^{2\pi} \int_{1}^{\sqrt{5}} (r^3\cos^2(\theta) + r^2\sin(\theta)) \, dr \, d\theta \\ & = \int_0^{2\pi} \left[\frac{r^4}{4}\cos^2(\theta) + \frac{r^3}{3}\sin(\theta)\right]_1^{\sqrt{5}} \, d\theta \\ & = \int_0^{2\pi} \left(6\cos^2(\theta) + \frac{5\sqrt{5}-1}{3}\sin(\theta)\right) \, d\theta \\ & = \int_0^{2\pi} \left(3 + 3\cos(2\theta) + \frac{5\sqrt{5}-1}{3}\sin(\theta)\right) \, d\theta \\ & = \left[3\theta + \frac{3\sin(2\theta)}{2} - \frac{5\sqrt{5}-1}{3}\cos(\theta)\right]_0^{2\pi} \\ & = 6\pi \end{split} \end{equation*}\]

Vamos a hacer que trabaje un poco nuestro oráculo de confianza. Con la ayuda de Sympy, vamos a comprobar que los cálculos realizados en el ejemplo anterior son correctos:

import sympy as sp

x, y, r, th = sp.symbols('x y r th', real=True) # define las variables simbólicas x, y, r, th

# Definimos las funciones F y G como matrices
F = sp.Matrix([ r*sp.cos(th), r*sp.sin(th) ])
G = sp.Matrix([ x**2 + y ])

# Definimos la nueva función a integrar 
GoF_expr = G.subs(x,r*sp.cos(th)).subs(y,r*sp.sin(th))

# Calculamos el determinante de la matriz jacobiana asociada a F
det_jac_F = sp.det( F.jacobian([r,th]) )

# Calculamos la integral sobre la nueva región de integración
res = sp.integrate(GoF_expr*abs(det_jac_F), (r, 1, sp.sqrt(5)), (th, 0, 2*sp.pi))
# res = sp.integrate(GoF_expr[0]*abs(det_jac_F), (r, 1, sp.sqrt(5)), (th, 0, 2*sp.pi))
display('Valor de la integral: ')
display(sp.simplify(res[0]))
# display(sp.simplify(res))

'Valor de la integral: '
\[\displaystyle 6 \pi\]