1.8. Coordenadas cilíndricas y esféricas#
Hasta ahora hemos utilizado las coordenadas cartesianas para representar punto, rectas y superficies en \(\mathbb{R}^{3}\). Es decir, caracterizamos cada punto por sus coordenadas respecto a los tres ejes cartesianos: \((x,y,z).\) En esta sección vamos a estudiar otras dos maneras de describir un punto con las coordenadas cilíndricas y esféricas, lo que, en ocasiones, nos permitirá simplificar la escritura.
1.8.1. Coordenadas cilíndricas#
El sistema de coordenadas cilíndricas es una extensión de las coordenadas polares en el plano al espacio 3D. Mantendremos las coordenadas polares en el plano \(XY\) añadiendo la altura \(Z\). Es decir:
Definition (Coordenadas cilíndricas)
En un sistema de coordenadas cilíndricas un punto \(P\) del espacio se representa por medio de una terna ordenada \(\left(r,\theta,z\right)\), donde:
\((r,\theta)\) es una representación en coordenadas polares de la proyección de \(P\) sobre el plano \(XY\).
\(z\) es la distancia dirigida de \((r,\theta)\) a \(P\).
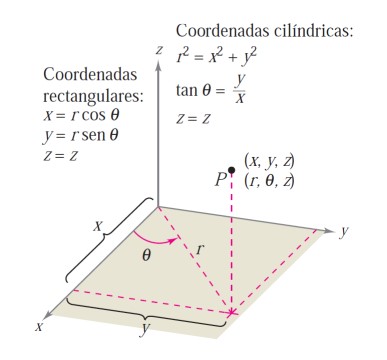
Para realizar los cambios de coordenadas, de cartesianas a cilíndricas y viceversa, aplicaremos las siguientes fórmulas:
Cartesianas a cilíndricas:
\(r = \sqrt{x^2+y^2}\), \(\theta = \arctan\left(\frac{y}{x}\right)\), \(z=z\).
Cilíndricas a cartesianas:
\(x = r\cos(\theta)\), \(y=r\sin(\theta)\), \(z=z\).
El punto \((0,0,0)\) se llama polo u origen de coordenadas. Además, dado que la representación del origen en \(\mathbb{R}^{2}\) no es única en polares, tampoco será única la representación del origen en \(\mathbb{R}^{3}\) en coordenadas cilíndricas.
Las coordenadas cilíndricas son especialmente convenientes para representar superficies cilíndricas y superficies de revolución con el eje \(Z\) como eje de simetría, como mostramos en la figura a continuación:
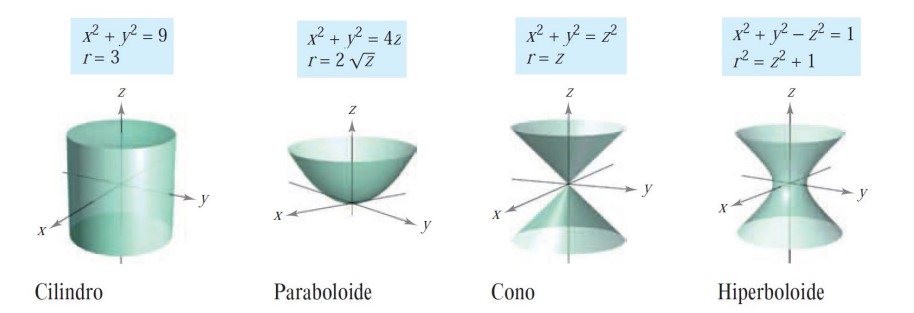
También los planos verticales y horizontales tienen ecuaciones simples en coordenadas cilíndricas:
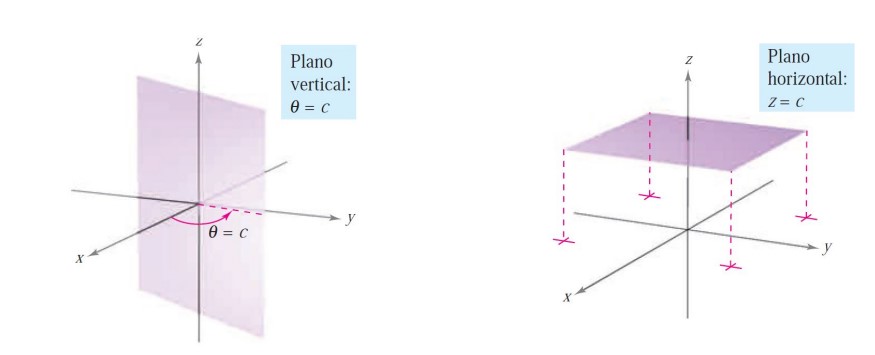
1.8.2. Coordenadas esféricas#
En el sistema de coordenadas esféricas cada punto, \(P\), está representado por 3 coordenadas: la primera es la distancia desde \(P\) al origen, la segunda el ángulo que forma la proyección de \(P\) sobre el plano \(XY\) (esta segunda es igual que en las coordenadas cilíndricas) y la tercera el ángulo que forma \(OP\) con el eje \(Z\). Es decir:
Definition (Coordenadas cilíndricas)
En un sistema de coordenadas esféricas un punto \(P\) del espacio se representa por medio de una terna ordenada \(\left(\rho,\theta,\phi\right)\), donde:
\(\rho\) es la distancia entre \(P\) y el origen (\(\rho \geq 0\)).
\(\theta\) es el mismo ángulo utilizado en coordenadas cilíndricas para \(r\geq 0\).
\(\phi\) es el ángulo entre el eje \(Z\) positivo y el segmento de recta \(OP\) (\(0\leq \phi \leq \pi\)).
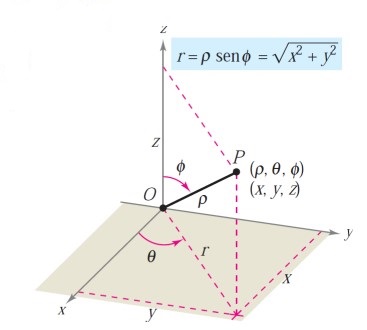
Para realizar los cambios de coordenadas, de cartesianas a esféricas y viceversa, aplicaremos las siguientes fórmulas:
Cartesianas a esféricas:
\(\rho = \sqrt{x^2+y^2+z^2}\), \(\theta = \arctan\left(\frac{y}{x}\right)\), \(\phi = \arccos\left(\frac{z}{\sqrt{x^2+y^2+z^2}}\right)\).
Esféricas a cartesianas:
\(x = \rho\sin(\phi)\cos(\theta)\), \(y=\rho\sin(\phi)\sin(\theta)\), \(z=\rho\cos(\phi)\).
Si nos interesa cambiar de cilíndricas a esféricas, o viceversa:
Esféricas a cilíndricas:
\(r^2 = \rho^2 \sin^2(\phi)\), \(\theta = \theta\), \(z = \rho\cos(\phi)\).
Cilíndricas a esféricas:
\(\rho = \sqrt{r^2+z^2}\), \(\theta = \theta\), \(\phi=\arccos\left( \frac{z}{\sqrt{r^2+z^2}} \right)\).
El sistema de coordenadas esféricas es útil, sobre todo, en superficies en \(\mathbb{R}^3\) que tienen un punto o un eje de simetría. Por ejemplo:
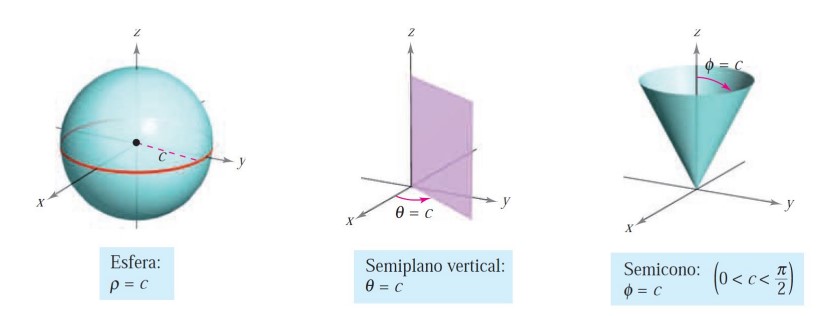
Como curiosidad, podemos comentar que el sistema de longitud-latitud, que se usa en posicionamiento GPS para describir un punto en la superficie de la Tierra, corresponde a una variante (el ángulo \(\phi\) se mide desde el plano) de las coordenadas esféricas:
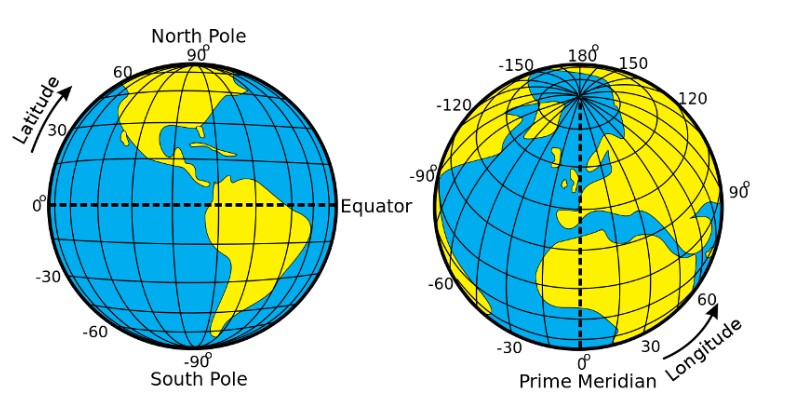
Por ejemplo…
Si quieres enterarte más de esto, puedes consultar, por ejemplo: https://world.ubergizmo.com/es/como/aprende-a-leer-las-coordenadas-del-gps/.
1.8.3. Algunos ejercicios resueltos con Python#
Vamos a ver a continuación algunos ejercicios/ejemplos de cambios de coordenadas.
Ejercicio 1: Pasar el punto \(P_{1} = (x,y,z) = (3,5,4)\) a coordenadas cilíndricas y esféricas.
Ejercicio 2: Pasar el punto \(P_{2} = (r,\theta,z) = (2,\frac{\pi}{4},-3)\) a coordenadas cartesianas y esféricas.
Ejercicio 3: Pasar el punto \(P_{3} = (\rho,\theta,\phi) = (2,\frac{\pi}{4},\frac{\pi}{4})\) a coordenadas cartesianas y cilíndricas.
# Resolvemos el ejercicio 1. Dejamos 2 y 3 para que practiquéis
import numpy as np
def cart_2_cil(P):
r = np.sqrt(P[0]**2+P[1]**2)
theta = np.arctan(P[1]/P[0])
z = P[2]
return r,theta,z
def cart_2_esf(P):
rho = np.sqrt( P[0]**2+P[1]**2+P[2]**2 )
theta = np.arctan(P[1]/P[0])
phi = np.arccos( P[2]/rho )
return rho,theta,phi
P_car = np.zeros(3)
P_cil = np.zeros(3)
P_esf = np.zeros(3)
# Dato
P_car = np.array([3., 5., 4.])
# Cambiamos de coordenadas
P_cil = cart_2_cil(P_car)
P_esf = cart_2_esf(P_car)
print('Dato: P_car= ', P_car)
print('P_cil= ',P_cil)
print('P_esf= ',P_esf)
Dato: P_car= [3. 5. 4.]
P_cil= (5.830951894845301, 1.0303768265243125, 4.0)
P_esf= (7.0710678118654755, 1.0303768265243125, 0.9695321101157683)
Ahora nos vamos a quedar en el cálculo simbólico (es decir, en Sympy), para cambiar de coordenadas la ecuación de una superficie.
Ejercicio 4: Representa en coordenadas cilíndricas y esféricas la ecuación del cono \(x^2+y^2=z^2\).
Ejercicio 5: Representa en coordenadas cilíndricas y esféricas la superficie que en coordenadas cartesianas se representa como \(x^2+y^2+z^2-4z=0\).
# Resolvemos el ejercicio 4 y os dejamos el 5 para que practiquéis
import sympy as sp
x = sp.Symbol('x')
y = sp.Symbol('y')
z = sp.Symbol('z')
r = sp.Symbol('r', nonnegative = True)
theta = sp.Symbol('theta')
rho = sp.Symbol('rho', nonnegative = True)
phi = sp.Symbol('phi')
# Definimos la ecuación en cartesianas
exp_cart = x**2+y**2 - z**2
ec_cart = sp.Eq(exp_cart,0)
# Pasamos la ecuación a cilíndricas
ec_cil = ec_cart.subs({x:r*sp.cos(theta), y:r*sp.sin(theta), z:z})
display(sp.simplify(ec_cil))
# Pasamos la ecuación a esféricas
ec_esf = ec_cart.subs({x:rho*sp.sin(phi)*sp.cos(theta), y:rho*sp.sin(phi)*sp.sin(theta), z:rho*sp.cos(phi)})
display(sp.simplify(ec_esf))

