1.2. Vectores en el espacio#
En esta (breve) sección generalizaremos las ideas de la anterior, escrita para vectores en \(\mathbb{R}^2\), al espacio tridimensional, \(\mathbb{R}^3\).
1.2.1. Coordenadas en el espacio#
Para identificar puntos en el espacio 3D necesitaremos un sistema de coordenadas tridimensional. Para ello consideramos un eje \(Z\) perpendicular a los dos ejes, \(X\) e \(Y\), como se muestra en la siguiente figura:
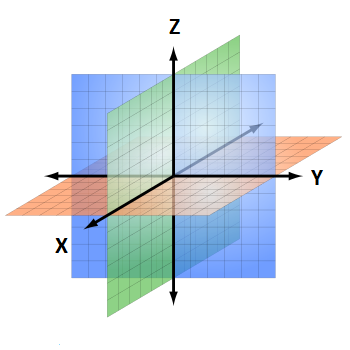
Puedes consultar más información sobre esto en la Wiki (página de la que hemos sacado la figura anterior): https://es.wikipedia.org/wiki/Sistema_de_coordenadas.
Con el sistema que estamos eligiendo, se separa el espacio en ocho octantes (fíjate que en 2D hay cuatro cuartos): el primero de estos octantes corresponde a la zona en la que las tres coordenadas son positivas.
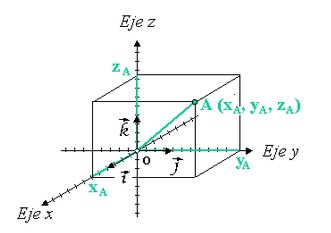
Entonces, un punto, \(P\), en el espacio se caracteriza por un triple ordenado, \((x,y,z)\), donde:
\(x\) es la distancia desde el plano \(YZ\) a \(P\),
\(y\) es la distancia desde el plano \(XZ\) a \(P\),
\(z\) es la distancia desde el plano \(XY\) a \(P\).
NOTA: Elegiremos siempre un sistema de coordenadas dextrógiro: el giro corto desde la parte positiva del eje \(X\) hacia la parte positiva del eje \(Y\) iría en el sentido contrario a las agujas del reloj (como en 2D). Puedes ver más detalles aquí, jugando con la conocida regla de la mano derecha o regla del sacacorchos: https://en.wikipedia.org/wiki/Right-hand_rule.
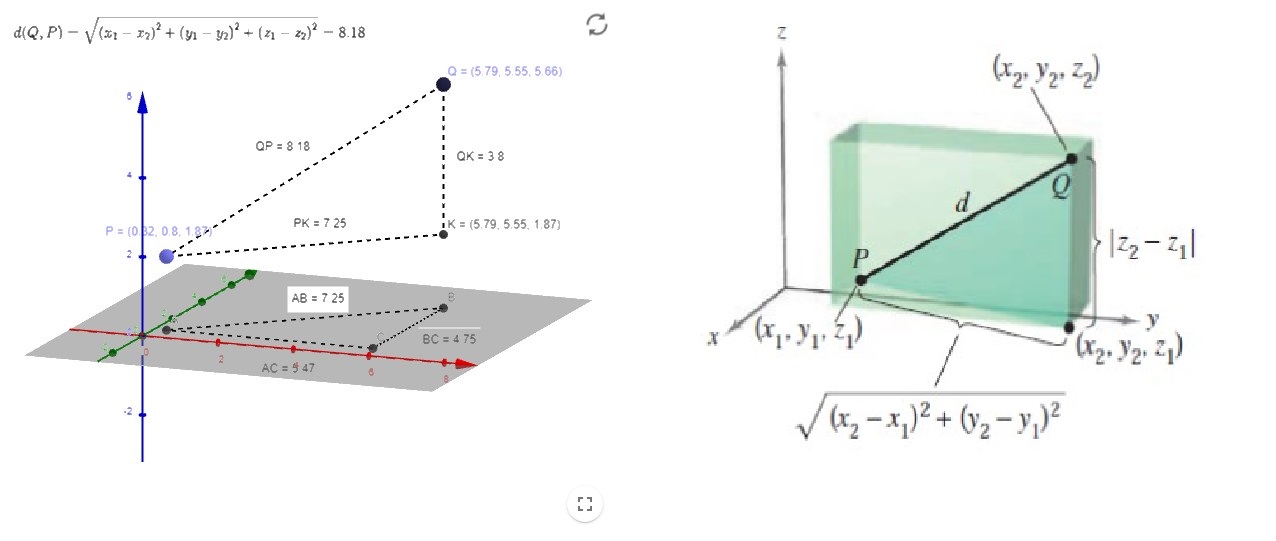
1.2.2. Distancia en el espacio#
Para encontrar la distancia entre dos puntos en el espacio, podemos utilizar el Teorema de Pitágoras dos veces, para obtener:
Esperamos que la siguiente figura te ayude. Si no fuera así, puedes jugar con la siguiente aplicación en Geogebra: https://www.geogebra.org/m/QjnTG76X.
1.2.3. Ecuación de la esfera#
Las esferas en 3D juegan un papel similar a las circunferencias en 2D. Serán importantes a lo largo de este curso. Por eso mismo, vamos a dedicar unos minutos a definirlas correctamente.
Definition (Esfera)
La esfera de centro \(\left(x_{0}, y_{0}, z_{0}\right)\) y de radio \(r\) es el conjunto de puntos en \(\mathbb{R}^3\) que están a una distancia \(r\) de \(\left(x_{0}, y_{0}, z_{0}\right)\).
Es decir, utilizando la fórmula anterior para la distancia, es el conjunto de puntos \((x,y,z)\in\mathbb{R}^3\) tales que
o, equivalentemente y más usada en la práctica,
1.2.4. Vectores en el espacio#
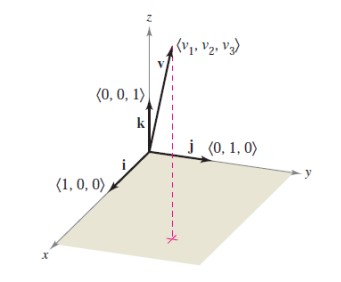
Al igual que hacíamos en la sección anterior para vectores en el plano, ahora, en el espacio, denotaremos los vectores por ternas ordenadas, \(\left(v_{1}, v_{2}, v_{3}\right)\), y lo abreviaremos con una letra en negrita, \(\mathbf{v}\) (utiliza una letra con una flecha encima cuando escriba a mano, \(\vec{v}\)). Además:
El vector cero se denota: \(\mathbf{0}=(0,0,0)\).
Los vectores canónicos unitarios serán: \(\mathbf{i}=(1,0,0)\), \(\mathbf{j}=(0,1,0)\) y \(\mathbf{k}=(0,0,1)\).
La notación estándar para un vector puede escribirse: \(\mathbf{v} = v_{1}\mathbf{i} + v_{2}\mathbf{j} + v_{3}\mathbf{k}\).
De nuevo, análogamente a lo que pasa en 2D, si \(\mathbf{v}\) está representado por el segmento de recta dirigido desde \(P = \left(p_{1}, p_{2}, p_{3}\right)\) hasta \(Q = \left(q_{1}, q_{2}, q_{3}\right)\), entonces
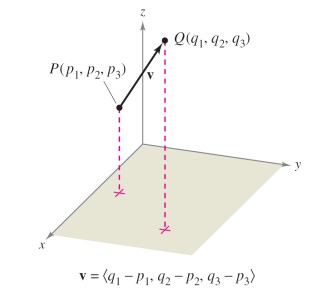
De todos modos, al igual que en el plano, la forma canónica de un vector es la que tiene como punto inicial el centro de coordenadas, \(\mathbf{0} = (0,0,0)\).
La longitud de un vector será
A diferencia de lo que sucede en el plano, ahora no basta con un ángulo para definir la dirección de un vector. Necesitamos dos ángulos. Suelen elegirse:
\(\theta\) en la proyección del vector en el plano \(XY\),
\(\phi\) para indicar el ángulo que forma el vector con el eje \(Z\).
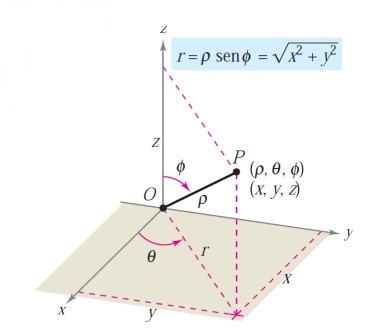
Profundizaremos más en esto cuando hablemos de coordenadas esféricas (véase Coordenadas cilíndricas y esféricas).
Ahora podemos definir el vector unitario en la dirección de \(\mathbf{v}\) como
Y, de forma totalmente análoga a los vectores en el plano, definimos las operaciones con vectores en el espacio:
Definition (Suma de vectores y multiplicación por un escalar en 3D)
Sean \(\mathbf{u}=\left( u_{1}, u_{2}, u_{3} \right)\) y \(\mathbf{v}=\left( v_{1}, v_{2}, v_{3} \right)\) vectores y sea \(c\in\mathbb{R}\) un escalar.
El múltiplo escalar de \(c\) y \(\mathbf{u}\) es el vector \(c\mathbf{u} := \left( cu_{1}, cu_{2}, cu_{3}\right)\).
La suma vectorial de \(\mathbf{u}\) y \(\mathbf{v}\) es el vector \(\mathbf{u}+\mathbf{v} := \left( u_{1} + v_{1}, u_{2} + v_{2}, u_{3} + v_{3}\right)\).
Relacionado con el producto escalar, recordemos que
El resultado de multiplicar el vector \(\mathbf{v}\) por el escalar \(c\) tiene la misma dirección que \(\mathbf{v}\) si \(c\) es positivo y la opuesta si \(c\) es negativo.
Dos vectores distintos de \(\mathbf{0}\), \(\mathbf{u}\) y \(\mathbf{v}\), se dicen paralelos si existe algún escalar \(c\) tal que \(\mathbf{u} = c\mathbf{v}\).
1.2.5. Jugando con vectores 3D en Numpy#
¡Venga! Vuelve a leer la Sección Introducción a Numpy y vamos a jugar un poco…
import numpy as np
# Definimos los vectores u y v
u = np.array([2, -7, 3])
v = np.array([1, -7/2, 3/2])
w = np.array([1, -3, 3/2])
# Calculamos la norma de u con la función de NumPy np.linalg.norm
norm_u = np.linalg.norm (u)
print('u: ', norm_u)
print('Norma de u: ', norm_u)
# Calculamos el vector unitario en la dirección de u
u1 = u/norm_u
print('Vector unitario en la dirección de u: ', u1)
# Comprobamos si u y v son paralelos
c = u[0]/v[0]
log = (u == c*v)
if log.all():
print('u y v son paralelos con razón u/v= ',c)
else:
print('u y v no son paralelos')
# Comprobamos si u y w son paralelos
c = u[0]/w[0]
log = (u == c*w)
if log.all():
print('u y w son paralelos con razón u/w= ',c)
else:
print('u y w no son paralelos')
u: 7.874007874011811
Norma de u: 7.874007874011811
Vector unitario en la dirección de u: [ 0.25400025 -0.88900089 0.38100038]
u y v son paralelos con razón u/v= 2.0
u y w no son paralelos

