3.8. Aplicaciones del cálculo de extremos#

En esta sección, vamos a practicar un poco estas últimas secciones y, de paso, a ver algunas aplicaciones del cálculo de extremos relativos y absolutos:

  1. En primer lugar, trataremos de obtener un modelo lineal que ajuste una colección de datos, mediante el método de mínimos cuadrados.

  2. En segundo lugar, resolveremos un problema de optimización, calculando extremos absolutos en un dominio compacto.

  3. Distancia de un punto a una superficie.

3.8.1. Método de mínimos cuadrados#

Al construir un modelo matemático para representar un fenómeno particular, los objetivos son simplicidad y precisión. Existen varias maneras para desarrollar tales modelos, tal vez la más importante sea el método de mínimos cuadrados.

En la wikipedia puedes ver una descripción completa de este método, desarrollado por Gauss a la avanzada edad de 18 años (aquí puedes conocer algo más de la vida del GENIO alemán).

La idea es que para saber cuánto se ajusta el modelo \(y = f(x)\) a la colección de puntos

\[ \{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\} \]

se puede calcular el cuadrado de la distancia entre los datos de los que se parte y los valores predichos por el modelo para obtener la suma de los errores al cuadrado o el error cuadrático:

\[ S = \sum_{i = 1}^n [f(x_i) - y_i]^2. \]

Esto es en general. De la elección de \(f\) que hagamos surgirán distintos métodos de mínimos cuadrados. Tal vez la elección más habitual es suponer que \(f\) es un polinomio de grado \(1\) (o sea, una recta). Aparece entonces la llamada recta de regresión, que es la recta que minimiza el error cuadrático para una colección de puntos. Lee aquí, si quieres saber más cosas de la recta de regresión.

Nosotros vamos a calcularla, como aplicación de lo que hemos aprendido en este tema.

Se trata de minimizar el error cuadrático tomando como función \(f\) una recta genérica, \(f(x) = ax +b\), y buscar los parámetros \(a\) y \(b\) que minimicen dicho error. Entonces:

\[ S(a,b) = \sum_{i = 1}^n [ax_i + b - y_i]^2, \]

donde \(a, b \in \mathbb{R}\).

Para obtener los valores de \(a\) y \(b\) que minimizan \(S\) tenemos que buscar los puntos críticos, es decir, los valores \(a\) y \(b\) que hacen que las dos derivadas parciales de \(S\),

\[\begin{split} \left\{\begin{array}{rcl} \dfrac{\partial S}{\partial a}(a,b) &=& \displaystyle 2\sum_{i = 1}^n x_i (ax_i + b - y_i) \\ \dfrac{\partial S}{\partial b}(a,b) &=& \displaystyle 2\sum_{i = 1}^n (ax_i + b - y_i) \end{array}\right. \end{split}\]

valgan \(0\):

\[\begin{split} \left\{\begin{array}{rcl} \displaystyle 2\sum_{i = 1}^n x_i (ax_i + b - y_i) &=& 0 \\ \displaystyle 2\sum_{i = 1}^n (ax_i + b - y_i) &=& 0 \end{array}\right. \Longrightarrow \left\{\begin{array}{ccccccl} \displaystyle a\sum_{i = 1}^n x_i^2 &+& \displaystyle b \sum_{i = 1}^n x_i &-& \displaystyle\sum_{i = 1}^n x_i y_i &=& 0 \\ \displaystyle a\sum_{i = 1}^n x_i &+& b n &-& \displaystyle\sum_{i = 1}^n y_i &=& 0 \end{array}\right. \end{split}\]

En resumen: hemos obtenido un sistema de dos ecuaciones con dos incógnitas del que se despejan \(a\) y \(b\) para obtener el siguiente teorema:

Theorem (Recta de regresión de mínimos cuadrados)

La recta de regresión de mínimos cuadrados para \(\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}\) está dada por \(f(x) = ax + b\), donde

\[\begin{split} \left\{\begin{array}{rcl} a &=& \frac{\displaystyle n \sum_{i=1}^{n}x_iy_i - \sum_{i=1}^{n}x_i\sum_{i=1}^{n}y_i}{\displaystyle n \sum_{i=1}^{n}x_i^2 - \left(\sum_{i=1}^{n}x_i\right)^2}, \\ \\ b &=& \displaystyle \frac{1}{n}\left(\sum_{i=1}^{n}y_i - a\sum_{i=1}^{n}x_i\right), \end{array}\right. \end{split}\]

Veamos un caso práctico.

Example

Hallar la recta de regresión de mínimos cuadrados para los puntos \((-3,0), (-1,1), (0,2)\) y \((2,3)\).

Solución:

A partir del resultado teórico anterior, tenemos que

\[ a = \frac{\displaystyle n \sum_{i=1}^{n}x_iy_i - \sum_{i=1}^{n}x_i\sum_{i=1}^{n}y_i}{\displaystyle n \sum_{i=1}^{n}x_i^2 - \left(\sum_{i=1}^{n}x_i\right)^2} = \dfrac{4(5) - (-2)(6)}{4(14) - (-2)^2} \]

y

\[ b = \frac{1}{n}\left(\sum_{i=1}^{n}y_i - a\sum_{i=1}^{n}x_i\right) = \frac{1}{4}\left[6 - \frac{8}{3}(-2)\right] = \frac{47}{26}. \]

Por tanto, la recta de regresión de mínimos cuadrados es

\[ f(x) = \frac{8}{13}x + \frac{47}{26}. \]

Vamos a preguntarle a nuestro oráculo por si nos hemos equivocado.

import sympy as sp
import numpy as np

x, y = sp.symbols('x y', real=True) # define las variables simbólicas x e y

# Datos
xi = np.array([-3, -1, 0, 2])
yi = np.array([0, 1, 2, 3])

# Cálculo de la recta de regresión
n = len(xi) # número de datos
a = (n*np.dot(xi,yi) - np.sum(xi)*np.sum(yi))/(n*np.sum(xi**2) - np.sum(xi)**2) 
b = (np.sum(yi) - a*np.sum(xi))/n

print('Recta de regresión: \n\n', y, ' = ', a*x + b)

Recta de regresión: 

 y  =  0.615384615384615*x + 1.80769230769231

3.8.2. Extremos absolutos en un dominio compacto#

Example (Cálculo de volumen máximo )

Una caja rectangular descansa sobre el plano \(XY\) con un vértice en el origen. El vértice opuesto se encuentra en el plano

\[ 6x + 4y + 3z = 24. \]
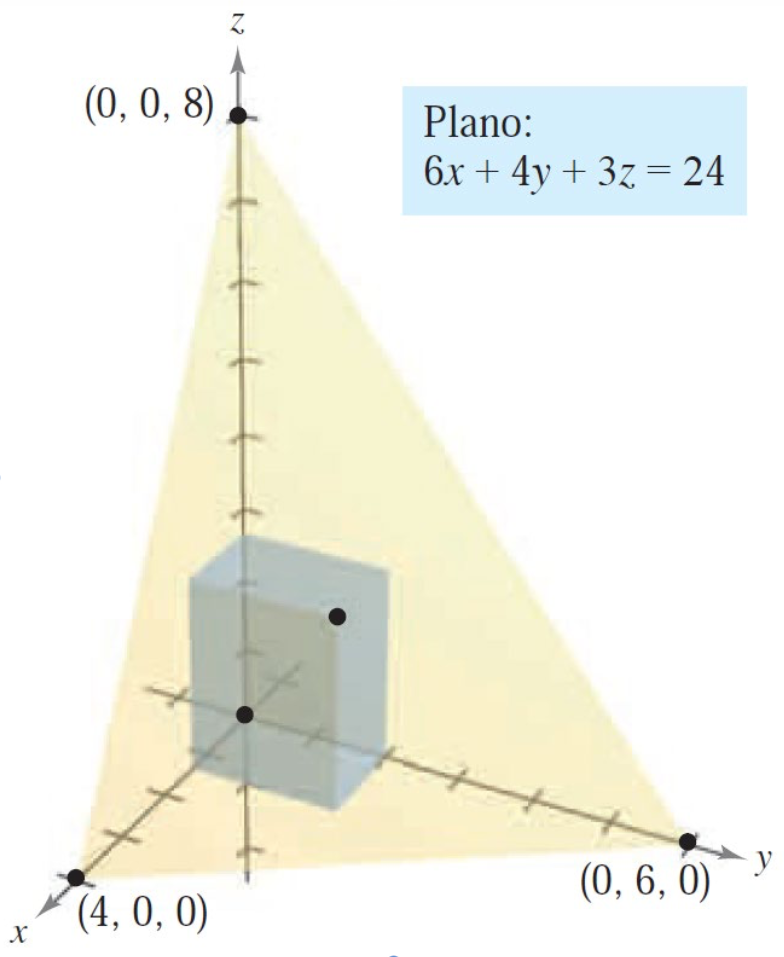
../../_images/3.8.Volumen_maximo.png

¿Cuál es el volumen máximo que puede tener la caja?

Solución:

Supongamos que \(x, y, z\) representan la longitud, anchura y altura de la caja. Debido a que un vértice de ella se encuentra en el plano \(6x + 4y + 3z = 24\), podemos despejar \(z\) de la ecuación de éste,

\[ z = \frac{1}{3}(24 - 6x - 4y), \]

para escribir el volumen de la caja, \(V = xyz\), en función de sólo dos variables:

\[ V(x,y) = x y \left(\frac{1}{3}\left(24 - 6x - 4y\right)\right) = \frac{1}{3}\left( 24xy - 6x^2y - 4xy^2\right). \]

A continuación, calculamos el gradiente de \(V\):

\[\begin{split} \mathbf{\nabla} V (x,y) = \frac{1}{3} \begin{bmatrix} 24y - 12xy - 4y^2 \\ \\ 24x - 6x^2 - 8xy\end{bmatrix} = \frac{2}{3}\begin{bmatrix} y(12 - 6x - 2y) \\ \\ x(12 - 3x - 4y)\end{bmatrix} . \end{split}\]

E igualamos a \(0\):

\[\begin{split} \left\{\begin{array}{rcl} y \left(12 - 6x - 2y\right) &=& 0 \\ \\ x \left(12 - 3x - 4y \right) &=& 0, \end{array}\right. \end{split}\]

se obtienen los puntos críticos \((0,0), (4,0), (0,6)\) y \(\left(\frac{4}{3},2\right)\).

En \((0,0), (4,0)\) y \((0,6)\), el volumen es \(0\), por lo que esos puntos no producen un volumen máximo.

En el punto \(\left(\frac{4}{3},2\right)\), se puede aplicar el criterio de la matriz hessiana. Como

\[\begin{split} \mathrm{Hess}V(x,y) = \begin{bmatrix} -4y & \frac{1}{3}(24 - 12x -8y) \\ \frac{1}{3}(24 - 12x -8y) & -\frac{8x}{3} \end{bmatrix}, \end{split}\]

entonces

\[\begin{split} \det\mathrm{Hess}V\left(\frac{4}{3},2\right) = \begin{vmatrix} -8 & -\frac{8}{3}\\ -\frac{8}{3} & -\frac{32}{9} \end{vmatrix} = \frac{64}{3} > 0, \end{split}\]

y \(\dfrac{\partial^2 V}{\partial {x^2}}(\frac{4}{3},2) = -8 < 0\), por lo que podemos concluir que \(V\) tiene un máximo relativo en \(\left(\frac{4}{3},2\right)\) y su valor es:

\[ V\left(\frac{4}{3},2\right) = \frac{1}{3}\left[24\left(\frac{4}{3}\right)(2) - 6\left(\frac{4}{3}\right)^2(2) - 4\left(\frac{4}{3}\right)(2^2)\right] = \frac{64}{9}. \]

¿Hemos terminado? No, porque faltaría comprobar el volumen en los puntos de la frontera del dominio triangular de \(V\). Comprueba que el volumen en estos puntos es igual a \(0\).

Ahora sí, podemos concluir que el volumen máximo es \(V\left(\frac{4}{3},2\right) = \frac{64}{9}\) unidades cúbicas.

Ya por último, vamos a resolver con Python el ejercicio propuesto.

import sympy as sp
import numpy as np
x, y = sp.symbols('x y', real=True) # define las variables simbólicas x e y
V = sp.Lambda((x,y), (24*x*y - 6*x**2*y -4 *x*y**2)/3)

# Calculamos el gradiente de f
grad_V =  sp.transpose(sp.Matrix([V(x,y)]).jacobian([x,y]))
display('Gradiente en (x,y): ', grad_V)

# Buscamos los puntos críticos
sol = sp.solve((sp.Eq(grad_V[0],0),sp.Eq(grad_V[1],0)),(x,y), dict = True)
display('Puntos críticos:', sol)

# V en (0,0), (4,0), (0,6) es igual a 0
print('V(0,0) =', V(sol[0][x],sol[0][y]), ', V(4,0) =', V(sol[3][x],sol[3][y]), 
      ', V(0,6) =', V(sol[1][x],sol[1][y]))

# Definimos la hessiana con sp.hessian
H = sp.Lambda((x,y), sp.hessian(V(x,y), (x,y)))
display('Matriz hessiana en (x,y): ', H(x,y))

# Clasificación del punto crítico (4/3,2)
H0 = H(sol[2][x],sol[2][y])
display('Hessiana del punto crítico (4/3,2): ', H0)
print("Determinante: ",sp.det(H0), ". Posición (1,1):", H0[0,0])

# V en (4/3,2) es igual a 64/9
print('\nEl volumen máximo de la caja es: \n\n V(4/3,2) =', V(sol[2][x],sol[2][y]))

'Gradiente en (x,y): '
\[\begin{split}\displaystyle \left[\begin{matrix}- 4 x y - \frac{4 y^{2}}{3} + 8 y\\- 2 x^{2} - \frac{8 x y}{3} + 8 x\end{matrix}\right]\end{split}\]
'Puntos críticos:'

[{x: 0, y: 0}, {x: 0, y: 6}, {x: 4/3, y: 2}, {x: 4, y: 0}]

V(0,0) = 0 , V(4,0) = 0 , V(0,6) = 0

'Matriz hessiana en (x,y): '
\[\begin{split}\displaystyle \left[\begin{matrix}- 4 y & - 4 x - \frac{8 y}{3} + 8\\- 4 x - \frac{8 y}{3} + 8 & - \frac{8 x}{3}\end{matrix}\right]\end{split}\]
'Hessiana del punto crítico (4/3,2): '
\[\begin{split}\displaystyle \left[\begin{matrix}-8 & - \frac{8}{3}\\- \frac{8}{3} & - \frac{32}{9}\end{matrix}\right]\end{split}\]
Determinante:  64/3 . Posición (1,1): -8

El volumen máximo de la caja es: 

 V(4/3,2) = 64/9

3.8.3. Distancia de un punto a una superficie#

Vamos a calcular la distancia desde un punto \((a,b,c)\) a una superficie definida mediante la ecuación

\[ g(x,y,z) = 0. \]

La distancia desde un punto fijo, \((a,b,c)\), a uno genérico \((x,y,z)\) es

\[ d((a,b,c),(x,y,z)) = \sqrt{(x-a)^2+(y-b)^2+(z-c)^2}. \]

Ahora bien, a la hora de buscar el mínimo, es más sencillo considerar la función \(d^2\) y así evitaremos la raíz cuadrada… y, sobre todo, sus derivadas que nos traerían una raíz cuadrada en el denominador. Pero, ¿podemos elegir \(d^2\) en vez de \(d\) sin modificar el problema (es decir, el mínimo está en el mismo sitio)?

La respuesta es sí, porque elevar al cuadrado, dentro de los números positivos, es una función estrictamente creciente y, por lo tanto, no altera el lugar en el que se alcanza el mínimo.

Por tanto, el problema puede escribirse como:

Example (Distancia de un punto a una superficie )

Minimizar la función

\[ f(x,y,z) = (x-a)^2 + (y-b)^2 + (z-c)^2 \]

sujeta a la restricción

\[ g(x,y,z) = 0. \]

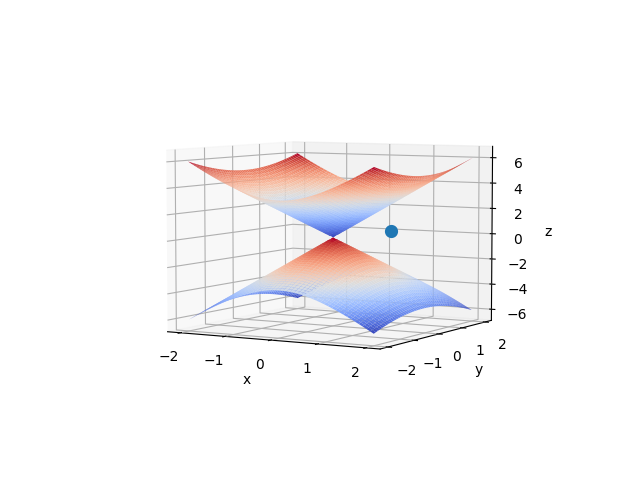
Veámoslo, con sympy, sobre un ejemplo: vamos a calcular la distancia desde el punto \(\left(1,\frac{1}{2},\frac{1}{2}\right)\) al cono \(\dfrac{z^2}{5^2}-\dfrac{x^2}{2^2}-\dfrac{y^2}{3^2} = 0\).

../../_images/3.8.Distancia.png 
import sympy as sp

x, y, z, l = sp.symbols('x y z l', real=True) # definimos las variables simbólicas x, y, l

a = 1; b = 0.5; c = 0.5
f = sp.Lambda((x,y,z), (x-a)**2+(y-b)**2+(z-c)**2) # función a optimizar
g_expr = z**2/5**2-x**2/2**2 - y**2/3**2
g = sp.Lambda((x,y,z), g_expr) # restricción

# Cálculo de puntos críticos (posibles extremos globales)
grad_f =  sp.transpose(sp.Matrix([f(x,y,z)]).jacobian([x,y,z]))
grad_g = sp.transpose(sp.Matrix([g(x,y,z)]).jacobian([x,y,z]))
sol = sp.solve((sp.Eq(grad_f[0],l*grad_g[0]),sp.Eq(grad_f[1],l*grad_g[1]),sp.Eq(grad_f[2],l*grad_g[2]), 
               sp.Eq(g(x,y,z),0)),(x,y,z,l), dict=True)

for p in sol:
    print('Punto crítico (x,y,lambda)=',p,'; distancia=', sp.N(sp.sqrt(f(p[x],p[y],p[z]))))

Punto crítico (x,y,lambda)= {l: 9.84374016275345, x: 0.288939257236422, y: 0.238806094816288, z: 0.824741732738127} ; distancia= 0.824188588240805