1.1. Vectores en el plano#

1.1.1. Definición de vector en el plano#

Muchas cantidades en geometría y física (área, volumen, temperatura, masa, tiempo,…) se pueden caracterizar por un único número real que se escala a las unidades de medida adecuadas (\(m^2\), \(m^3\), \(^\text{o}\)C,…). Se llaman magnitudes escalares, y al número real asociado con ellas se le llama escalar.

Sin embargo, otras cantidades (fuerza, velocidad, aceleración,…) implican magnitud y dirección y no pueden caracterizarse completamente por un solo número real: necesitaremos los vectores (y, más adelante, en algunos casos, las matrices).

De momento, vamos a centrarnos en dar una correcta definición para estas cantidades en el plano, \(\mathbb{R}^2\).

Definition

Llamaremos vector a un segmento en el plano, que estará caracterizado por el ángulo que forma con el eje \(OX\) (dirección) y por su longitud (o magnitud).

Suele representarse con una flecha con un punto inicial y un punto final en el plano, aunque esta representación puede dar lugar a confusiones, ya que dos segmentos con la misma longitud y dirección, aunque partan de puntos diferentes, definen el mismo vector.

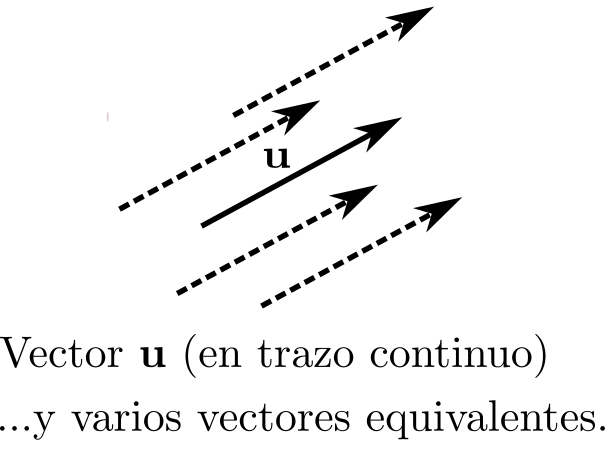
../../_images/01_vector_plano.png

A lo largo del presente libro denotaremos los vectores mediante letras minúscula y en negrita (\(\mathbf{n}\), \(\mathbf{u}\), \(\mathbf{v}\),… ), aunque cuando se escriben a mano suelen denotarse con una flecha (\(\vec{n}\), \(\vec{u}\), …).

Vamos a ver un ejemplo para que nos quede claro que dos segmentos con la misma dirección y longitud definen el mismo vector.

Example

Comprueba que, para los puntos \(P=(0,0)\), \(Q=(3,2)\), \(R=(1,2)\) y \(S=(4,4)\), los segmentos \(\vec{PQ}\) y \(\vec{SR}\) definen el mismo vector.

Vamos a comprobar que tienen la misma longitud y la misma pendiente (lo que implica que tendrán la misma dirección):

  • Longitud \(\vec{PQ}\): \(\sqrt{(3-0)^2+(2-0)^2} = \sqrt{13}\).

  • Longitud \(\vec{RS}\): \(\sqrt{(4-1)^2 + (4-2)^2} = \sqrt{13}\).

  • Pendiente que forma \(\vec{PQ}\) con la recta \(OX\): \(\frac{2-0}{3-0} = \frac{2}{3}\).

  • Pendiente que forma \(\vec{RS}\) con la recta \(OX\): \(\frac{4-2}{4-1} = \frac{2}{3}\).

../../_images/01_ejemplo1.png

Una vez aclarado que hay muchos segmentos que representan al mismo vector, conviene unificar esto. Por ello, entre todos los vectores con la misma longitud y dirección, suele elegirse el que tiene como punto de inicio el origen de coordenadas, \((0,0)\). Entonces, si entendemos que el punto inicial será el \((0,0)\), basta dar el punto final, \(Q=\left(v_{1}, v_{2}\right)\), para tener totalmente identificado un vector \(\mathbf{v}\).

Definition (Definición de un vector mediante sus componentes )

Definiremos \(\mathbf{v}\) como un vector en el plano mediante las coordenadas, \(\left( v_{1}, v_{2}\right)\), de su punto final, entendiendo que el punto inicial es el origen \((0,0)\). En este sentido, identificaremos vectores en el plano con elementos del espacio \(\mathbb{R} \times \mathbb{R} = \mathbb{R}^2\).

Las componentes \(v_{1}\) y \(v_{2}\) son las componentes de \(\mathbf{v}\).

Si el punto inicial y el punto final están ambos en el origen, entonces decimos que \(\mathbf{v}\) es el vector cero (o vector nulo) y se denota por \(\mathbf{0}= (0,0)\).

La longitud de \(\mathbf{v}\) se llama norma de \(\mathbf{v}\),

\[ \|\mathbf{v}\| = \sqrt{v_{1}^2+v_{2}^2}. \]

Si \(\|\mathbf{v}\| = 1\) diremos que \(\mathbf{v}\) es un vector unitario.

Además, \(\|\mathbf{v}\| = 0\) si y sólo si \(\mathbf{v} = \mathbf{0}\).

1.1.2. Operaciones vectoriales#

Definition (Suma de vectores y multiplicación por un escalar )

Sean \(\mathbf{u}=\left( u_{1}, u_{2}\right)\) y \(\mathbf{v}=\left( v_{1}, v_{2}\right)\) vectores y sea \(c\in\mathbb{R}\) un escalar.

  1. El múltiplo escalar de \(c\) y \(\mathbf{u}\) es el vector \(c\mathbf{u} := \left( cu_{1}, cu_{2}\right)\).

  2. La suma vectorial de \(\mathbf{u}\) y \(\mathbf{v}\) es el vector \(\mathbf{u}+\mathbf{v} := \left( u_{1} + v_{1}, u_{2} + v_{2}\right)\).

Veamos algunas consideraciones geométricas para estas operaciones:

El múltiplo escalar, \(c\mathbf{u}\), de un vector, \(\mathbf{u}\), es un vector que tiene módulo \(|c|\) veces \(\|\mathbf{u}\|\) y la misma dirección si \(c\) es positivo mientras que, para \(c\) un número negativo, direcciones opuestas. Lo ilustramos en la siguiente figura:

../../_images/01_multiplicacion_escalar.png

La suma de vectores, \(\mathbf{u}+\mathbf{v}\), puede entenderse gráficamente como la diagonal del paralelogramo que tiene como lados adyacentes \(\mathbf{u}\) y \(\mathbf{v}\), o, equivalentemente, como el resultado de colocar el segundo de los vectores en la punta del primero.

../../_images/01_suma_vectores.png

En consecuencia, podemos también interpretar gráficamente la resta de vectores jugando con el paralelogramo resultante.

../../_images/01_resta_vectores.png

Theorem (Desigualdad triangular )

Sean \(\mathbf{u}\), \(\mathbf{v}\in\mathbb{R}^2\). Entonces

\[ \|\mathbf{u}+\mathbf{v}\| \leq \|\mathbf{u}\| + \|\mathbf{v}\|. \]

La igualdad sólo se cumplirá si \(\mathbf{u}\) y \(\mathbf{v}\) tienen la misma dirección.

Theorem (Propiedades de la suma de vectores y multiplicación por escalar )

Sean \(\mathbf{u}\), \(\mathbf{v}\), \(\mathbf{w}\in\mathbb{R}^2\) y \(c\), \(d\in\mathbb{R}\). Entonces:

\[\begin{split} \begin{array}{ll} \textrm{1.}\; \mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u} & \textrm{(propiedad conmutativa).} \\ \textrm{2.}\; (\mathbf{u} + \mathbf{v}) + \mathbf{w} = \mathbf{u} + (\mathbf{v} + \mathbf{w}) & \textrm{(propiedad asociativa).} \\ \textrm{3.}\; \mathbf{u} + \mathbf{0} = \mathbf{u} & \textrm{(elemento neutro para la suma).} \\ \textrm{4.}\; \mathbf{u} + (-\mathbf{u}) = \mathbf{0} & \textrm{(elemento inverso para la suma).} \\ \textrm{5.}\; c(d\mathbf{u}) = (cd)\mathbf{u} & \textrm{(pseudo-asociativa).} \\ \textrm{6.}\; (c+d)\mathbf{u} = c\mathbf{u} + d\mathbf{u} & \textrm{(distributiva (1) ).} \\ \textrm{7.}\; c(\mathbf{u}+\mathbf{v}) = c\mathbf{u} + c\mathbf{v} & \textrm{(distributiva (2)).} \\ \textrm{8.}\; 1(\mathbf{u}) = \mathbf{u} & \textrm{(elemento neutro de la multiplicación por escalares).} \\ \textrm{9.}\; 0(\mathbf{u}) = \mathbf{0} & \textrm{(elemento 0 en la multiplicación por escalares).} \end{array} \end{split}\]

Al cumplirse estas nueve propiedades podemos afirmar que el espacio de vectores, con la suma y la multiplicación por escalares así definidas, forman un espacio vectorial.

1.1.3. Vectores unitarios#

Dado un vector \(\mathbf{u}\), muchas veces es importante calcular otro vector en la misma dirección y que tenga módulo \(1\) (es decir, que sea unitario). Lo definimos a continuación:

Definition (Vector unitario )

Sean \(\mathbf{u}\in\mathbb{R}^{2}\). Definimos \(\mathbf{u}_{1}\in\mathbb{R}^{2}\), el vector unitario en la dirección de \(\mathbf{u}\) como

\[ \mathbf{u}_{1} = \frac{\mathbf{u}}{\|\mathbf{u}\|} = \frac{1}{\|\mathbf{u}\|} \mathbf{u}. \]

Por su definición, es evidente que \(\|\mathbf{u}_{1}\| = 1\).

Dentro de todas las infinitas direcciones que existen en \(\mathbb{R}^2\) vamos a destacar dos de ellas, las llamadas direcciones canónicas, que nos permitirán utilizar una representación cartesiana del plano. Vamos a definir a continuación los vectores unitarios en estas direcciones:

Definition (Vectores unitarios canónicos )

Llamaremos vectores unitarios canónicos a

  1. \(\mathbf{i} = (1,0)\),

  2. \(\mathbf{j} = (0,1)\).

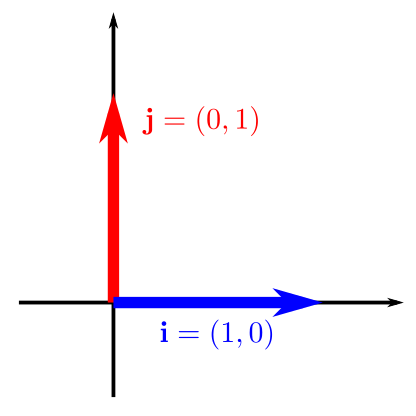
../../_images/01_vectores_canonicos.png

Una vez que ya hemos definido los evctores canónicos unitarios, podemos escribir cualquier vector, utilizando sus coordenadas, en función de éstos:

\[ \mathbf{u} = \left(u_{1}, u_{2}\right) = u_{1} (1,0) + u_{2} (0,1) = u_{1}\mathbf{i} + u_{2}\mathbf{j}. \]

1.1.4. Jugando con vectores en Sympy y Numpy#

Ahora deberías leerte las secciónes Introducción a SymPy y Introducción a Numpy para poder jugar un poco con las propiedades que acabas de aprender de vectores y con las librerías Sympy y Numpy, que utilizaremos a lo largo del presente curso. Te damos alguna pista:

import numpy as np

# Definimos los vectores u y v
u = np.array([1, 2])
v = np.array([3, 4])

# Imprimimos en pantalla estos vectores
print('u: ',u)
print('v: ',v)

# Sumamos los vectores, almacenando el resultado en w1
w1 = u + v
print('u+v: ', w1)

# Multiplicamos u por 3, v por -2 y los sumamos en w2
w2 = 3*u - 2*v
print('3u - 2v: ', w2)

u:  [1 2]
v:  [3 4]
u+v:  [4 6]
3u - 2v:  [-3 -2]

En Sympy hay que definir los vectores como matrices unidimensionales. En general, será útil si queremos mantener fracciones o queremos realizar cálculos simbólicos sobre los vectores:

import sympy as sp

x = sp.Symbol('x', real=True)

# Definimos los vectores u y v
u = sp.Matrix([sp.frac('1/2'), sp.frac('1/3')])
v = sp.Matrix([sp.frac('1/5'), 1])
w = sp.Matrix([1/x, x**2])

# Sumamos los vectores, almacenando el resultado en w1
w1 = u + v
print('u+v: ', w1)
# Queda más chulo con display:
display(w1)

# Multiplicamos w por 3
display('3w:',3*w)

u+v:  Matrix([[7/10], [4/3]])
\[\begin{split}\displaystyle \left[\begin{matrix}\frac{7}{10}\\\frac{4}{3}\end{matrix}\right]\end{split}\]
'3w:'
\[\begin{split}\displaystyle \left[\begin{matrix}\frac{3}{x}\\3 x^{2}\end{matrix}\right]\end{split}\]

Ahora puedes aprovechar la potencia de cualquiera de estas librerías (tampoco es que sea muy necesaria para lo que se avecina, pero…) y resolver el siguiente problema:

Example 1.1

Si dos remolcadores empujan un petrolero, el primero con una fuerza de módulo 8000 HP en la dirección \((1,-1)\) y el segundo con una fuerza de 10000 HP en la dirección \((1,1)\).

  1. ¿Cuál es la magnitud y la dirección resultante del empuje de los 2 remolcadores?

  2. Si el primer remolcador aumentara su empuje un 50 %, manteniendo la misma dirección, ¿cuál sería la fuerza resultante?