1.5. El producto triple#

En esta sección definiremos el producto triple, también llamado producto mixto o producto triple escalar.

1.5.1. Definición#

Definition (Producto triple)

Sean \(\mathbf{u}\), \(\mathbf{v}\) y \(\mathbf{w}\in\mathbb{R}^3\) vectores arbitrarios. Definimos su producto triple como el número real

\[ \left[\mathbf{u}, \mathbf{v}, \mathbf{w}\right] := \mathbf{u} \cdot \left(\mathbf{v} \times \mathbf{w} \right). \]

Este número puede calcularse resolviendo el siguiente determinante:

\[\begin{split} \left[\mathbf{u}, \mathbf{v}, \mathbf{w}\right] = \left| \begin{array}{ccc} u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \\ w_{1} & w_{2} & w_{3} \end{array} \right|. \end{split}\]

1.5.2. Interpretación geométrica#

El producto triple de los vectores \(\mathbf{u}\), \(\mathbf{v}\) y \(\mathbf{w}\) es igual al volumen de un paralelepípedo que tiene a estos vectores como aristas adyacentes, como se puede visualizar en la aplicación de Geogebra, creada por Ignacio Larrosa Cañestro, https://www.geogebra.org/m/ZKCrbEdt, de la que extraemos la siguiente imagen:

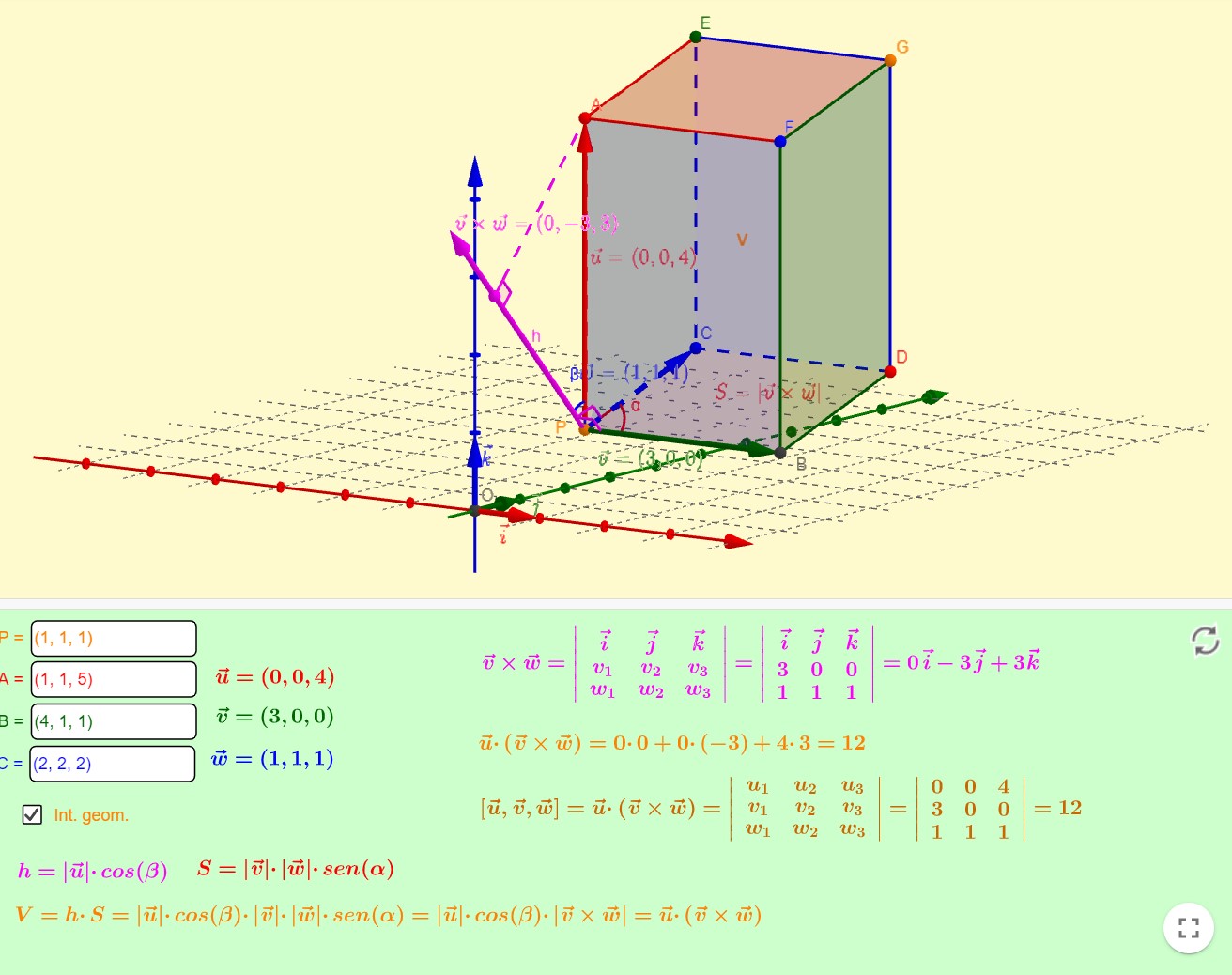
../../_images/1.5.producto_triple.jpg

Observemos que, como es evidente, el volumen de este paralelepípedo será \(0\) si y sólo si los tres vectores \(\mathbf{u}\), \(\mathbf{v}\) y \(\mathbf{w}\) están en el mismo plano. Por lo tanto, a la inversa, podemos afirmar que \(\mathbf{u}\), \(\mathbf{v}\) y \(\mathbf{w}\) serán coplanarios si y sólo si \(\displaystyle \left[\mathbf{u}, \mathbf{v}, \mathbf{w}\right] = 0\).

1.5.3. Script en Python#

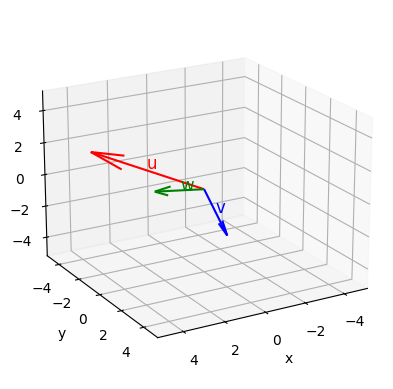
Vamos a hacer, ayudados por Numpy un ejemplo de esta operación entre vectores. Calcularemos el producto triple de los vectores \(\mathbf{u}=(3,-5,1)\), \(\mathbf{v}=(0,2,-2)\) y \(\mathbf{w}=(3,1,1)\).

import numpy as np
import matplotlib as mp
import matplotlib.pyplot as plt

# Definimos los vectores u, v y w
u = np.array([3, -5, 1])
v = np.array([0, 2, -2])
w = np.array([3, 1, 1])

# Calculamos su producto vectorial de v y w
producto_vectorial = np.cross(v,w)
# Calculamos el producto escalar de u contra este producto vectorial
producto_triple=np.dot(u,producto_vectorial)

print('Producto triple: ', producto_triple)

# Inicialización de la representación 3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Representación de los vectores
ax.quiver([0], [0], [0], np.array([u[0], v[0], w[0]]), np.array([u[1], v[1], w[1]]), np.array([u[2], v[2], w[2]]), color=['r','b','g','r','r','b','b','g','g'])

# Añadimos etiquetas a los vectores
ax.text(u[0]/2, u[1]/2, u[2]/2+0.1, 'u', fontsize=12, color='r')
ax.text(v[0]/2, v[1]/2, v[2]/2, 'v', fontsize=12, color='b')
ax.text(w[0]/2, w[1]/2, w[2]/2, 'w', fontsize=12, color='g')

# Ajuste de los límites de los ejes
ax.set_xlim([-5,5])
ax.set_ylim([-5,5])
ax.set_zlim([-5,5])

# Etiquetas de los ejes
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

# Orientamos los ejes
ax.azim = 60
ax.elev = 20

plt.show()

Producto triple:  36
../../_images/05.ProductoTriple_1_1.png

1.5.4. Más información#

Puedes encontrar más información del producto triple en: